Упражнение 5. Разложение выражений в ряд Тейлора

Используется команда Символика – Переменная – Разложить в ряд.

Разложение выражения в ряд Тейлора проводится относительно выделенной переменной с заданным по запросу числом членов ряда n. Такое разложение относительно точки х = х₀ функции f(x) имеет вид:

f(x) = f(x₀) + + + +…+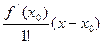

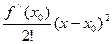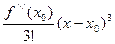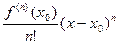
Если разложение выполняется относительно точки х = 0, то такой ряд называется рядом Маклорена, и он имеет вид:

f(x) = f(0) + + + + …. +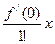

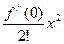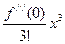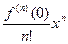
По умолчанию n принимает значение равное 6. В разложении указывается остаточная

погрешность.

Вычисление ряда Тейлора для функции .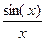

Исходное выражение Результат операции

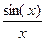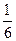1- ·x²+ 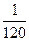·x⁴+0(x⁵)

Построение графиков функций:

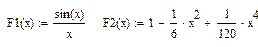
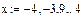
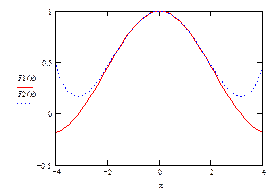
Разложения в ряд Тейлора используется для вычисления определенного интеграла, который в явном виде не берется.

Рассмотрим интеграл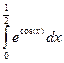

Данный интеграл можно вычислить методом Симпсона, используя знак вывода =

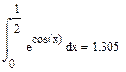
Данный интеграл можно вычислить также путем замены подынтегральной функции ее разложением в ряд Тейлора.

Разложение функции e^cos(x) в ряд Тейлора с 10 членами имеет вид:

e^cos(x) = exp(1)+ 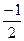·exp(1)·x² + 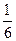·exp(1)·x⁴ + 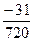·exp(1)·x⁶ + 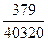·exp(1)·x⁸ + 0(x¹⁰).

C помощью операций Copy (копирование в буфер обмена) и Paste (вставка из буфера объмена) подставим первые четыре члена разложения в качестве подынтегральной функции, в результате получим:

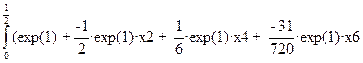)dx = 1.305