Метод наименьших квадратов: алгоритм метода; условия применения

В матем статистике методы получения наилучшего приближ к исходным данным в виде аппроксимирующей функции назыв регрессионным анализом. Его основн задачами явл установление завис-сти между переменными и оценка(прогноз)значений завис переменной.

При оценивании пар-ров регр.моделей наиболее часто применяется МНК. Его оценки обладают такими стат. св-вами: несмещенность, состоятельность, эффективность. Достоинство МНК: простота мат.выводов и вычислит-х процедур.

Пусть имеем выборку из 4-х точек (n=4):

P₁ =(x₁, y₁),P₂ =(x₂, y₂), P₃ =(x₃, y₃), P₄ =(x₄, y₄)

Предполагаем, что существует теоретическая прямая, которая наилучшим образом проходит через них. Задача: оценить с некоторой точностью, как может проходить эта прямая

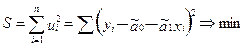Итак, оценки параметров модели парной регрессии согласно МНК будем искать из условия:

Задача оценки параметров парной регр.модели МНК сводится к задаче определения экстремума (минимума) ф-ии 2х аргументов

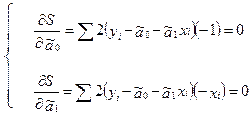Система называется системой нормальных уравнений для вычисления оценок параметров уравнения парной регрессии. Упростим систему нормальных уравнений.

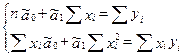
Убеждаемся, что решение системы уравнений будет соответствовать минимуму функции.

Для этого вычисляем значения вторых частных производных функции

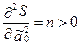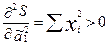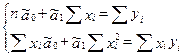Для решения системы выразим из первого уравнения ã₀, подставим его во второе уравнение. Получим:

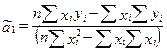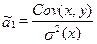Проанализируем выражение. Для этого вычислим COV(x,y) и σ²(x).Получим:

Проверим выполнение условия несмещенности для оценки. Для этого вычислим числитель выражения.Получаем: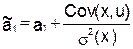

Вычислим дисперсии параметров уравнения регрессии и дисперсию прогнозирования эндогенной переменной.