Тестирование моделей на наличие гетероскедастичности, тест ранговой корреляции

В основу идей тестов моделей на присутствие гетероскедастичности лежит предположение о том, что гетероскедастичность есть результат зависимости дисперсий случайных возмущений от абсолютных значений регрессоров. Для более проверки применяют различные статистические тесты, такие как: Тест Уайта, Тест Голдфелда-Куандта, Тест Бройша — Пагана, Тест Парка, Тест Глейзера, Тест ранговой корреляции Спирмэна. Тест ранговой корреляции Спирмена. В основу теста также положено предположение о том, что дисперсия случайного возмущения связана с абсолютными значениями регрессоров. Тест Спирмена основан на вычислении коэффициента ранговой корреляции между случайными возмущениями и абсолютными значениями вектора 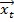. 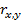= 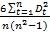где: n – объем выборки; D_t – разность между рангами по абсолютным значениям вектора 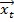и случайного возмущения u_t. В случае отсутствия гетероскедастичности, значение коэффициента ранговой корреляции 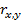должен равняться нулю, т.е. основная гипотеза принимает вид H₀: 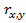= 0.Т.к. закон распределения случайной переменной 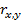не известен, то для тестирования гипотезы формируется случайная переменная: r_расч=r_x,y* 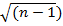_. Случайная переменная r_расч подчиняется нормальному закону распределения N(0; 1/(n-1)), при условии, что r_расч=0. Для нормального распределения можно вычислить для заданной доверительной вероятности критического значение r_крит и, если выполняется условие r_расч < r_крит, то нулевая гипотеза об отсутствии гетероскедастичности принимается.