В соответствии со второй предпосылкой теоремы Гаусса-Маркова нужно соблюдение условия гомоскедастичности, или однородности, или одинаковости дисперсий случайных возмущений во всех наблюдениях: 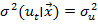 . Если это условие не соблюдается, то имеет место гетероскедастичность. Распределение u для каждого наблюдения имеет нормальное распределение и нулевое ожидание, но дисперсия распределений различна. Последствия нарушения условия гомоскедастичности случайных возмущений: 1. Потеря эффективности оценок коэффициентов регрессии, т.е. можно найти другие, отличные от МНК и более эффективные оценки. 2. Смещенность стандартных ошибок коэффициентов в связи с некорректностью процедур их оценки. Это, в свою очередь, может привести к некорректности результатов тестирования статистической значимости параметров линейной модели.
. Если это условие не соблюдается, то имеет место гетероскедастичность. Распределение u для каждого наблюдения имеет нормальное распределение и нулевое ожидание, но дисперсия распределений различна. Последствия нарушения условия гомоскедастичности случайных возмущений: 1. Потеря эффективности оценок коэффициентов регрессии, т.е. можно найти другие, отличные от МНК и более эффективные оценки. 2. Смещенность стандартных ошибок коэффициентов в связи с некорректностью процедур их оценки. Это, в свою очередь, может привести к некорректности результатов тестирования статистической значимости параметров линейной модели.
Подход к решению проблемы устранения гетероскедастичности сводится к искусственному преобразованию спецификации модели таким образом, чтобы условие гомоскедастичности выполнялось тождественно. Пусть спецификация модели: Yt=a0+a1x1t+a2x2t+a3x3t+ut. Способ 1. Частный случай, когда известны дисперсии случайных возмущений в каждом наблюдении: Делится каждое уравнение наблюдений на свое σ(ut) и получается: 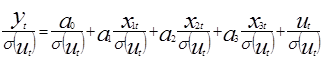 Тогда дисперсия случайного возмущения в каждом уравнении наблюдений есть:
Тогда дисперсия случайного возмущения в каждом уравнении наблюдений есть: 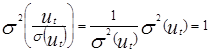 . Модель в каждом уравнении наблюдения имеет одинаковые дисперсии случайного возмущения равные 1. Недостаток способа – оценить σ(ut) на практике не возможно! Способ 2. Предполагаем, что σ(ut)=λxkt, где xkt регрессор «вызывающий» гетероскедастичность. Пусть для примера это регрессор x2t. Уравнение делится на значение этого регрессора:
. Модель в каждом уравнении наблюдения имеет одинаковые дисперсии случайного возмущения равные 1. Недостаток способа – оценить σ(ut) на практике не возможно! Способ 2. Предполагаем, что σ(ut)=λxkt, где xkt регрессор «вызывающий» гетероскедастичность. Пусть для примера это регрессор x2t. Уравнение делится на значение этого регрессора: 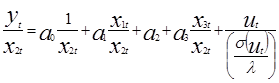 .Дисперсия случайного возмущения при этом есть:
.Дисперсия случайного возмущения при этом есть: 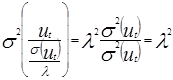 . Уравнения модели имеют постоянную дисперсию случайного возмущения равную λ2. Если регрессоров, приводящих к гетероскедастичности, несколько, то делается предположение:
. Уравнения модели имеют постоянную дисперсию случайного возмущения равную λ2. Если регрессоров, приводящих к гетероскедастичности, несколько, то делается предположение: 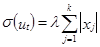 . Обе части модели делятся на величину Σ│xj│:
. Обе части модели делятся на величину Σ│xj│: 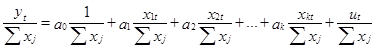 . Тогда дисперсия случайного возмущения полученной модели есть:
. Тогда дисперсия случайного возмущения полученной модели есть: 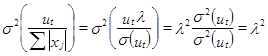 . Способ 3. Взвешенный метод наименьших квадратов: Предполагается, что дисперсию случайного возмущения можно представить в виде:
. Способ 3. Взвешенный метод наименьших квадратов: Предполагается, что дисперсию случайного возмущения можно представить в виде:
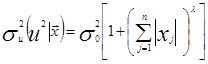 где:
где: 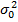 – дисперсия единицы веса, λ – заданная константа, например ±0.5; ±1; ±2. Вес случайного остатка вычисляется по правилу:
– дисперсия единицы веса, λ – заданная константа, например ±0.5; ±1; ±2. Вес случайного остатка вычисляется по правилу: 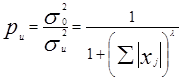 . Если в схеме Гаусса-Маркова не выполняется предпосылка о гомоскедастичности случайных возмущений, то наилучшей линейной процедурой оценки параметров модели является:
. Если в схеме Гаусса-Маркова не выполняется предпосылка о гомоскедастичности случайных возмущений, то наилучшей линейной процедурой оценки параметров модели является: 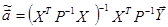 . где: Р матрица ковариаций случайных возмущений в уравнения наблюдений:
. где: Р матрица ковариаций случайных возмущений в уравнения наблюдений: 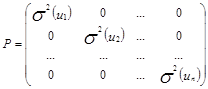
 2015-05-18
2015-05-18 1958
1958








