Метод наименьших квадратов минимизирует сумму квадратов отклонений реальных наблюдений за эндогенной переменной от её значения, рассчитанного по модели. Является методом решения задачи: оценить неизвестные параметры регресс.модели, проверить гипотезы об их значимости и адекватности модели анализируемому эк.объекту.
МНК позволяет находить оценки, обеспеч.макс.точность (мин.дисперсию) в классе несмещённых и линейно связанных с наблюдениями y оценками.
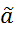 мнк = arg min
мнк = arg min 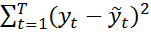 ,
,
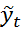 - оценённое (подстановочное) значение энд.пер-ной от включения оценок неизвестных параметров
- оценённое (подстановочное) значение энд.пер-ной от включения оценок неизвестных параметров 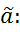
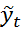 =
= 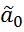 +
+ 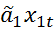 +…+
+…+ 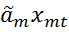 .
.
Тогда критерием качества оценивания явл. сумма квадратов реально зарегистрированных и подстановочных значений: 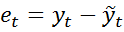 - остаток (отклонение)модели.
- остаток (отклонение)модели.
МНК-оценки: 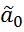 мнк =
мнк = 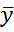 -
- 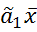 ,
, 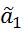 мнк =
мнк = 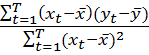 ,
,
где 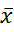 =
= 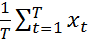 ,
, 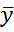 =
= 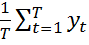 .
.
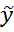 =
= 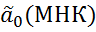 +
+ 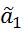 (МНК)*х.
(МНК)*х.
Оптимальность оценок МНК означает наличие свойств:
1) оценки а0 и а1 имеют нормальные вероятностные законы распределения и обладают свойством несмещённости, т.е. мат.ожидание оценки = соотв. характеристике генеральной совокупности (искомому параметру): M{ 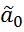 } =
} = 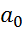 , M{
, M{ 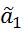 } =
} = 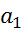 .
.
Если св-во нарушается, возникает смещённость b=M 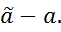
M{ 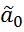 (МНК)}=
(МНК)}= 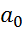 +
+  ΣM{
ΣM{ 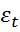 }=
}= 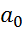 ;
;
Дисперсия этой оценки: D{ 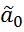 (МНК)} = D{
(МНК)} = D{ 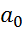 } +
} + 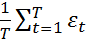 = =
= = 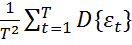 =
= 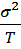 . Но т.к. она неизвестна=>
. Но т.к. она неизвестна=>
Дисперсию заменяют несмещённой оценкой: 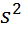 =
= 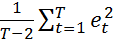 =
=  .
.
2)предел оценки с ростом выборки n равен истинному значению параметра: 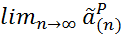 = a, P = (|
= a, P = (| 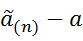 |<ε)→1.
|<ε)→1.
3) если 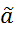 несмещённая, причём D
несмещённая, причём D 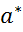 =minD
=minD 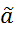 ,
, 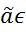 A, т.е. обладает равномерно-минимальной дисперсией, то
A, т.е. обладает равномерно-минимальной дисперсией, то 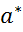 - эффективная (оптимальная).
- эффективная (оптимальная).
Фундаментальное свойство МНК: МНК-оценки параметров линейной регрессии обладают наименьшими дисперсиями среди множества всех несмещённых и линейно-зависимых от энд.перемен оценок в рамках модельных предположений 1-4. (Th Гаусса-Маркова)
Кроме точечных оценок использ. интервальные.
Доверительный интервал для 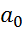 :
:
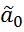 (МНК) -
(МНК) - 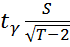 <
< 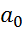 <
< 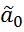 (МНК) +
(МНК) + 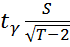 ,
,
γ = 1-α, α – уровень значимости, 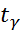 = St(T-2),
= St(T-2), 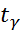 - квантиль по табл Стьюдента.
- квантиль по табл Стьюдента.
Доверительный интервал для 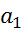 :
:
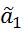 (МНК) -
(МНК) - 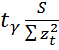 <
< 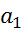 <
< 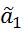 (МНК) +
(МНК) + 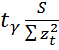 ,
,
где 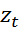 =
= 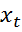 -
- 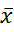 .
.
 2015-05-18
2015-05-18 498
498








