2015-05-18
474
y = f(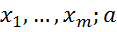
)+ε, где описывается зависимость одной эндогенной переменной от m (m>1) экзогенных переменных.
y =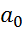 
+ 
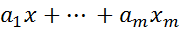+ ε.
Используют векторно-матричное представление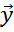 
= X 
.
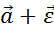X = 1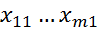 
, =(
)’, 
=(
)’, 
=(
)’,
::::::::::::::::
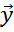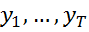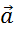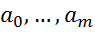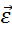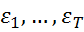1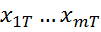 
По степени владения априорной информацией различ. 2 задачи:
1)при неизвестной функции взаимосвязи – задача подбора структуры модели.
2)при заданной функции – задача оценивания неизвестных параметров. Основной метод оценивания параметров - метод наименьших квадратов (минимизирует сумму квадратов отклонений реальных наблюдений за эндогенной переменной от её значения, рассчитанного по модели), кот.обеспечивает оптимальные свойства оценкам только при выполнении классических предположений:
П1. отсутствие систематич.ошибок наблюдений уравнения регрессии: M{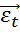 
} = 
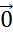, t=1,…,T.
П2. случайные ошибки некоррелированы между собой: M{εε'}=0.Коэфф корреляции: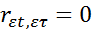 
.
П3. наблюдения производятся с одинаковой точностью, т.е. дисперсии случ. переменных одинаковы во все моменты измерения: D{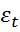 
} = 
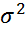, t=1,…,T.
П4. Экз.переменные измеряются без ошибок. В случае модели МЛР их значения образуют линейно-независимые векторы. det(X’X)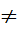 
0 =>rank(X) = min(T, m+1). Отсутствие мультикол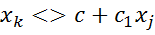 
П5. Ошибки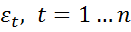 
имеют нормальное совместное распределение 
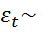N(0, ).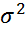
МНК-оценки находятся как решение задачи Q(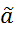
) = (
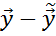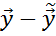)’ * () →min – квадратическая форма (где 
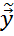= Х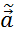 
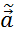, - вектор оценок множества неизвестных параметров 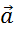) и имеют вид 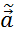(МНК) = 
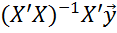- матричная форма.
