Кроме задачи оценивания параметров представляет интерес задача о значимости параметров, т.е. задача проверки отделимости параметров регрессии от нуля, которая решается проверкой статистических гипотез при выполнении классических предположений П1-П5:
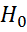 (
(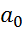 ):
): 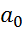 =0; где t(
=0; где t(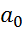 ) =
) = 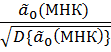 ;
;
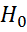 (
(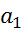 ):
): 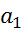 =0; где t(
=0; где t(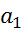 ) =
) = 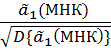 .
.
Решающее правило для проверки гипотез:
Если |t(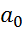 )|>
)|> 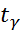 , где
, где 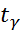 - квантиль распределения Стьюдента с надёжностью γ, то отклоняют гипотезу
- квантиль распределения Стьюдента с надёжностью γ, то отклоняют гипотезу 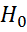 и делают вывод о существенной значимости параметра
и делают вывод о существенной значимости параметра 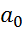 . Аналогично для
. Аналогично для 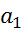 .
.
Вторая задача проверки качества модели основана на адекватности (обоснованность выбора принятой в соответствии с моделью регрессии взаимосвязи у и х). Мера адекватности – коэф. детерминации:
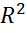 =
= 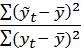 =
= 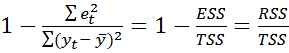 , гдеTSS – вся D, ESS – необъясненная часть D, RSS - объяснен. TSS= ESS+RSS
, гдеTSS – вся D, ESS – необъясненная часть D, RSS - объяснен. TSS= ESS+RSS
Часто используется скорректированныйкоэф.детерм. (с учётом степеней свободы): 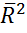 =
= 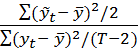 .
.
Решающее правило: Если 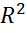 (T-2)/((1-
(T-2)/((1- 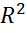 )/2) >
)/2) > 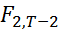 (γ), то отвергается гипотезе о неадекватности ПЛР (
(γ), то отвергается гипотезе о неадекватности ПЛР (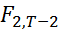 (γ) – квантиль порядка γ закона распределения Фишера).
(γ) – квантиль порядка γ закона распределения Фишера).
Если 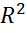 = 1, то ПЛР полностью отражает зависимость у от х. Все наблюдаемые точки
= 1, то ПЛР полностью отражает зависимость у от х. Все наблюдаемые точки 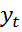 лежат на графике
лежат на графике 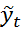 =
= 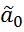 +
+ 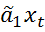 .Если
.Если 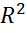 = 0, то модель неадекватна и информация о х не влияет на изменения у.
= 0, то модель неадекватна и информация о х не влияет на изменения у.
Нельзя придавать большое значение коэф-ту детерминации, надо дополнять проверку адекватности другими показателями; для ПЛР 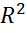 совпадает спарным коэф-том корреляции.
совпадает спарным коэф-том корреляции.
По модели ПЛР можно построить прогноз зависимой переменной уна горизонт будущего:
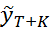 =
= 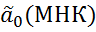 +
+ 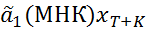 , где K – глубина прогноза в будущем,
, где K – глубина прогноза в будущем, 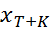 - планируемое в будущем моменте времени T+K значение факторной переменной. Чем дальше глубина прогноза, тем менее чётким он будет.Доверительный интервал прогноза:
- планируемое в будущем моменте времени T+K значение факторной переменной. Чем дальше глубина прогноза, тем менее чётким он будет.Доверительный интервал прогноза:
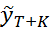 -
- 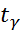 S
S 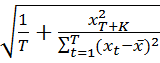 <
< 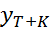 <
< 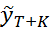 +
+ 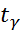 S
S 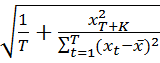 .
.
 2015-05-18
2015-05-18 390
390








