Методы устранения автокорреляции

Автокорреляция чаще всего вызывается неправильной спецификацией модели. Поэтому для её устранения необходимо, прежде всего, попытаться скорректировать саму модель. Также автокорреляция может быть вызвана отсутствием в модели некоторой важной объясняющей переменной. Необходимо попытаться определить данный фактор и учесть его в уравнении регрессии. Также можно попробовать изменить формулу зависимости. Однако если изменения спецификации модели всё же не помогли, то можно предположить, что автокорреляция обусловлена какими-то внутренними свойствами ряда{e_t}. В этом случае можно воспользоваться авторегрессионным преобразованием. В линейной регрессионной модели либо в моделях, сводящихся к линейной, наиболее целесообразным и простым преобразованием является авторегрессионная схема первого порядка AR(1).

Можно рассмотреть AR(1) на примере парной линейной регрессии:

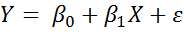
Наблюдениям tи (t-1) соответствуют формулы:

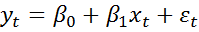
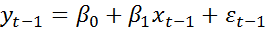
Пусть случайные отклонения подвержены воздействию AR(1):

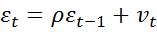, где 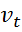, е = 2, 3, …, T–случайные отклонения, удовлетворяющие всем предпосылкам МНК, а коэффициент 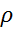известен.

Если из 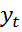вычесть 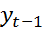умноженное на : .

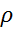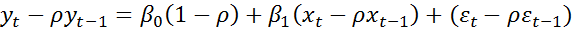Обозначив 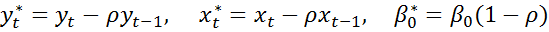и с учётом 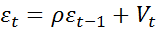, получается .

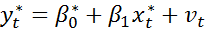Так как по предположению коэффициент 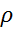известен, то 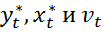вычисляются достаточно просто. Также, исходя их того, что случайные отклонения 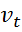удовлетворяют предпосылкам МНК, то оценки 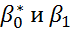будут обладать свойствами наилучших линейных несмещённых оценок.

Однако способ вычисления 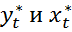приводит к потере первого наблюдения. Число степеней свободы уменьшится на единицу, что при больших выборках не так существенно, но при малых выборках может привести к потере эффективности. Это проблема обычно преодолевается с помощью поправки Прайса-Винстена:

,

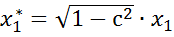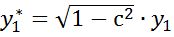
Авторегрессионное преобразование может быть использовано для уравнения множественной регрессии.

AR(1) может быть обобщено на преобразования более высоких порядков AR(2), AR(3) и т.д.: .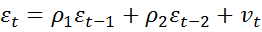

Однако на практике значение коэффициента 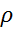обычно неизвестно и его необходимо оценивать. Существует несколько методов оценивания. Наиболее употребляемыми являются: 1) определение 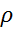на основе статистики Дарбина-Уотсана; 2) метод Кохрана-Оркатта; 3) метод Хилдрета-Лу; 4) метод первых разностей.

1) Статистика Дарбина-Уотсана тесно связана с коэффициентом корреляции между соседними отклонениями через соотношение:

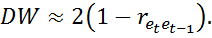
Исходя из этого, в качестве оценки коэффициента 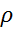может быть взят коэффициент 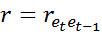. Получаем: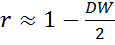

Этот метод оценивания используется при большом количестве наблюдений. В этом случае оценка 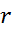параметра 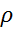будет достаточно точной.

2) Метод Кохрана-Оркатта является итерационным процессом. Его можно описать на примере парной регрессии 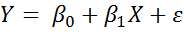и схемы AR(1) .

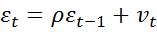1. Оценивается по МНК данная регрессия и для неё определяются оценки 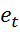отклонений 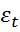, t = 1, 2, …,n.

2. Используя схему AR(1) оценивается регрессионная зависимость 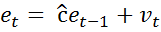, где 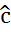– оценка коэффициента .

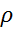3. На основе данной оценки строится уравнение:

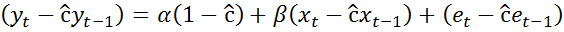
С его помощью оцениваются коэффициенты 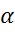и .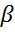

4. Значения 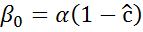и 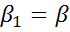подставляются в уравнение данной регрессии. Вновь вычисляются оценки 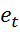отклонений и процесс возвращается к этапу 2.

Чередование этапов осуществляется до тех пор, пока не будет достигнута требуемая точность. То есть пока разность между предыдущей и последующей оценками 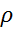не станет меньше любого наперёд заданного числа.

3) По методу Хилдрета-Лу регрессия 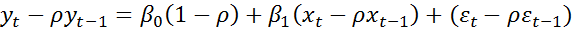оценивается для каждого возможного значения 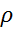из интервала [-1, 1] с любым шагом. Величина 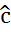, дающая наименьшую стандартную ошибку регрессии, принимается в качестве оценки коэффициента 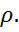И значения 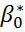и 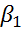оцениваются из данного уравнения регрессии именно с данным значением 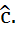Этот итерационный метод широко используется в эконометрических пакетах.

4) В случае, когда есть основания считать, что автокорреляция отклонений очень велика, можно использовать метод первых разностей. Для временных рядов характерна положительная автокорреляция остатков. Поэтому при высокой автокорреляции полагают 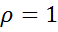. Следовательно: 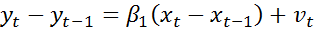, где 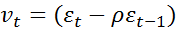. Обозначив 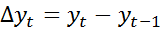, , 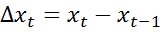получается 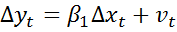. Из данного уравнения по МНК оценивается параметр 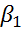. Коэффициент 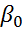в данном случае не определяется непосредственно. Однако из МНК известно, что .

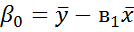В случае 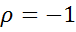, можно получить следующее уравнение регрессии: .

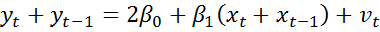Однако метод первых разностей предполагает уж слишком сильное упрощение (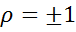), поэтому более предпочтительными являются итерационные методы.