Для выяснения того или иного случайного явления часто прибегают к высказыванию гипотез, которые можно проверить статистически, те опираясь на результаты наблюдений в случайной выборке.
Статистической гипотезой называют предположение о виде неизвестного закона распределения случайной величины или значения его параметра.
Предположим что надо проверить гипотезу о том, что 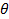 = 0 где
= 0 где 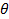 определенное число, причем задан закон распределения случайной величины Х зависящей от этого параметра.
определенное число, причем задан закон распределения случайной величины Х зависящей от этого параметра.
Проверяемую гипотезу обычно называют нулевой Н0. Гипотезу противоположную по смыслу нулевой называют альтернативной и обозначают Н1.
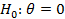
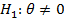
Следовательно множества выборок объемом Н можно разделить на 2 пересекающихся подмножества. Q W.
Если наблюдаемая выборка попадет под множество Q, то гипотеза Н0 должна быть принята, если под множество W – критическая область, а подмножество Q – область допустимых или вероятных значений.
Вывод о принадлежности данной выборки к соответствующему подмножеству делают по статистическому критерию.
Статистическим критерием называется однозначно определенное правило, устанавливающее условия при которых гипотезу Н0 следует либо отвергнуть или принять в качестве рабочей гипотезу. Основой критерия является специально составленная выборочная статистика закон распределения которого известен.
Вставить формулу 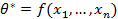
Если наблюдаемое значения статистика попала в критическую область W то гипотезу Н0 отвергают. Если же значения статистики критерия попала в допустимые значения то гипотезу Н0 принимают (не отвергают)
При использовании этого принципа могут быть 4 случая:
1) гипотеза Н0 верна и её принимают согласно критерию;
2) гипотеза Н0 неверна и её отвергают согласно критерию;
3) гипотеза Н0 верна, но её отвергают согласно критерию, т.е. допускается ошибка которую называют ошибкой первого рода
4) гипотеза Н0 неверна и её принимают согласно критерию называют ошибку второго.
Статистический критерий не доказывает, а только устанавливает на принятом уровне значимости её согласие или несогласие с данным критерием.
q = 90, 95, 99%
a=1-q= 10, 5, 1 %
Проверка гипотезы о статистической значимости линейного коэффициента корреляции по критерию Стьюдента.
Имеется выборочная совокупность (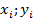 ). По известной формуле расчитывается линейный коэффициент корреляции.
). По известной формуле расчитывается линейный коэффициент корреляции.
Требуется с заданной доверительной вероятностью оценить статистическую значимость r выборочного те его отличие от 0.
1. Выдвигаем гипотезу Н0 что 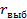 = 0. Альтернативная гипотеза Н1:
= 0. Альтернативная гипотеза Н1: 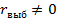
2. Задаемся величиной уровня значимости критерия A(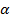 )=10% q=90% гипотеза Н0 принимается с доверительной вероятностью. Так как линейный коэффициент корреляции может принимать и положительные и отрицательные значения, то используется двухсторонний критерий.
)=10% q=90% гипотеза Н0 принимается с доверительной вероятностью. Так как линейный коэффициент корреляции может принимать и положительные и отрицательные значения, то используется двухсторонний критерий. 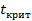 Вставка К – число степеней свободы.
Вставка К – число степеней свободы. 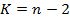 .
.
3. Поскольку известно, что статистика которая формируется по такому правилу вставить
Имеет распределение Стьюдента, то в качестве статистического критерия используется правило сравнения выборочной статистики Стьюдента с её критическим значением. 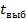 –вставка.
–вставка. 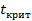 вычисляется по таблице. При этом могут быть 2 случая, если
вычисляется по таблице. При этом могут быть 2 случая, если 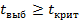 , то гипотеза отвергается, а если
, то гипотеза отвергается, а если 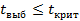 .
.
Семинарист: Складчиков Сергей Андреевич
 2015-05-18
2015-05-18 722
722








