2015-05-18
310
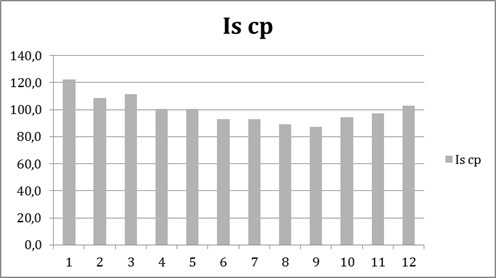
Пример расчета индекса сезонности на месячных данных потребления чего-то там.
| Месяцы | В среднем за 3 года 
| Внутригодовой средний индекс сезонности | |||
| Yi | Yi | Yi | Is | ||
| 165,7 | 122,4 | ||||
| 111,3 | |||||
| 150,7 | 100,4 | ||||
| 100,4 | |||||
| 92,8 | |||||
| 125,7 | 93,1 | ||||
| 89,1 | |||||
| 120,7 | 87,2 | ||||
| 94,5 | |||||
| 97,5 | |||||
| 131,7 | 97,3 | ||||
| 139,3 | 103,9 | ||||
| Общий средний уровень ряда | 138,8 | 135,6 | 131,8 | Yср=135,4 |
Если ряд динамики содержит тренд, то прежде чем вычислить сезонную волну тренд надо выделить используя аналитическое выравнивание ряда динамики.
Имеются данные об объёме электроэнергии жителей региона за 12 кварталов.
| Потреблении электроэнергии | |||||||||
| Yi | ti | ti^2 | Yi*ti | Yтеор | Is | Yi-Yтеор | (Yi-Yтеор)^2 | ||
| -11 | -66 | 5,38 | 111,6% | 0,62 | 0,39 | ||||
| 4,4 | -9 | -39,6 | 5,66 | 77,7% | -1,26 | 1,60 | |||
| -7 | -35 | 5,95 | 84,0% | -0,95 | 0,90 | ||||
| -5 | -45 | 6,23 | 144,3% | 2,77 | 7,65 | ||||
| 7,2 | -3 | -21,6 | 6,52 | 110,4% | 0,68 | 0,46 | |||
| 4,8 | -1 | -4,8 | 6,81 | 70,5% | -2,01 | 4,03 | |||
| 7,09 | 84,6% | -1,09 | 1,19 | ||||||
| 7,38 | 135,5% | 2,62 | 6,87 | ||||||
| 7,67 | 104,4% | 0,33 | 0,11 | ||||||
| 5,6 | 39,2 | 7,95 | 70,4% | -2,35 | 5,53 | ||||
| 6,4 | 57,6 | 8,24 | 77,7% | -1,84 | 3,37 | ||||
| 8,52 | 129,1% | 2,48 | 6,14 | ||||||
| Сумма | 83,4 | 81,8 | 83,40 | 0,00 | 38,23 | ||||
| Среднее | 6,95 | 47,67 | 6,82 | 6,95 | 0,00 | 3,19 |
| Годы | Кварталы | Ti | yi | yiti | T2i | ^yi | Индекс сезонности по каждому кварталу is | Индекс сезонности по одноименному кварталу I ср s |
| -11 | 6,0 | -66 | 108,63 | |||||
| -9 | 4,4 | -39,96 | ||||||
| -7 | 5,0 | |||||||
| -5 | 9,0 | |||||||
| -3 | 7,2 | |||||||
| -1 | 4,8 | |||||||
| 6,0 | ||||||||
| 10,0 | ||||||||
| 8,0 | ||||||||
| 5,6 | ||||||||
| 6,4 | ||||||||
| 11,0 | ||||||||
| Итого | ||||||||
| Среднее |
Необходимо построить математическую модель данного ряда выделить сезонную волну и определить прогноз потребления в течении 1 полугодия 2006 года.
1. выделим тренд в виде линейной функции ^y=a1+a2t. A1-ycp=6,95 a2=cp yi*ti/t2ср=0,14 y^=6,95+0,14t
2. Вычислить индексы сезонности по каждому кварталу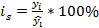 
3. Определить среднее значение индекса сезонности по одноименному кварталу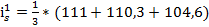 
4. Определим прогнозное значение потребления электроэнергии с учётом наличия тренда и сезонной волны. Осуществим точечный прогноз.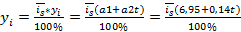 
5. Для прогнозирования подставим в модели прогнозное значение времени и прогнозный индекс сезонности
Интервальный прогноз
Поэтому его сопровождают значением средней ошибки прогноза и доверительным интервалом прогноза с требуемой доверительной вероятностью.
Под ошибкой понимается разность между его истинным значением и значением полученным по модели регрессии. Модуль этой разности будем называть предельной ошибкой.
Предельную ошибку определяют как произведение среднего на коэффициент статистики Стьюдента
Вставка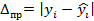 
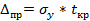
t – квантиль распределения Стьюдента
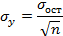
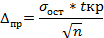
Сигма ост это среднее квадр отклонения результативного признака от линии регрессии
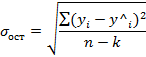
Тогда доверительные границы(интервальных границ) рассчитываются по следующей формуле
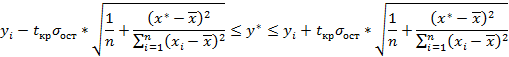
Понятие автокорреляции
При наличие в рядах динамики тренда и сезонных колебаний значение каждого уровня динамики как правило зависит от предыдущего уровня. Yt- текущий yt-1 – предыдущий, yt+1 – последующий
Эта зависимость носит отрицательный характер тк это приводит либо повышению либо к его понижению. Поэтому необходимо выявлять зависимость между уровнями ряда и учитывать её при моделировании. Корреляционная зависимость между последовательными (соседними) называется автокорреляцией уровней ряда.
Закономерность выражается в знаке каждой двух соседних отклонений от линии тренда. При положительной автокорреляции знаки отклонения от линии тренда попарно одинаковы. При отрицательной автокорреляции точки наблюдения поочередно отклоняются в разные стороны от линии регрессии.
Вставить графики
Количественные меры взаимосвязи между уровнями является коэффициент автокорреляции, который расчитывается по формуле линейного коэффициента корреляци
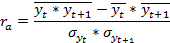
yt с чертой – это обозначение исзодного ряда
yt+1 средний уровень сдвинутого на 1 период ряда
Среднее из произведений уровня исходного ряда на один
Сигма yt и +1 среднее квадратическое отклонение рядов yt и yt+1
Следует заметить что коэффициент автокорреляции можно рассчитать как между соседними уровнями исходного ряда так и между уровнями ряда сдвинутыми друг относительно друга на любое число временных единиц. Такое временное смещение называется сдвигом или временным лагом.
Свойства коэффициентов автокорреляции:
1) -1<ra<1
2) по увеличению коэффициента автокорреляции можно судить о наличие линейной тенденции в нём
3) знак коэффициента автокорреляции указывает на вид автокореляции положительный или отрицательной
Если значение последнего уровня ряда мало отличается от первого уровня то сдвинутый ряд условно дополняют принимая yn=y1. В этом случае длины рядов сохряняются и средние значения для этих рядов будут равны друг другу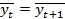 
кроме того будут равны и среднеквадратические отклонения поскольку они рассчитываются для рядов состоящих из одинаковых элементов. 
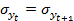. Формула упрощается
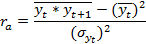
Рассмотрим пример имеются данные за 10 лет
Статистическая проверка значимости коэффициента автокорреляции.
Выдвигаем гипотезу H0 –
Фрагмент для уровня значиомостти
Следовательно ra > r крит что говорит о наличие автокорреляции ряда динамики.
Оказывается не только сами уровни но и отклонения отлинии тренлда могут автокоррелироватть.
Автокорреляция в отклонениях от тренда.
Не только уровня ряда динамики, но и отклонения от линии тренда могут коррелировать с уровнем динамики. Для выявления автокорреляции в отклонении используется критерий Дарбина-Уотсона. – DW.
Выборное начение критерия расчитывается по формуле
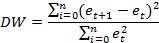
et=yt-^yt
В теории вероятности было доказано, что выборочная статистика ДВ была равна DW=2*(1-ra)
Из данной формулы следует:
1) если значение отклонений имеют сильную положительную автокорреляцию(ra->1), тогда критерий ДВ равен 0
2) при сильной отрицательной автокорреляции ra=-1 DW=4
3) ra=0 =>DW=2
Если автокорреляция положительна то критерий DW < 2
Если автокорреляция отрицательна то 2<DW<4
Критическое значение зависит от уровня значимости альфа, длины ряда динамики и от числа переменных модели. A; n; K
Значение статистика DW d1 и d2 при 5% уровне значимости.
При срванении выборочной статстики ДВ с критическими значениями Д1 и Д2 существуют следующие варианты:
1) для положительной корреляции Гипотеза об отстутсиви автокореляции отвергается те автокореляция в отклоеннии линии тренда есть
2) если больше Д2 то автокореляции в отклонениях нет ДВ>D2
3) между D1<DW<D2 нет достаточных оснований для приянятия решения
Для отрицательной автокорреляции с Д1 и Д2 сравниват (4-ДВ)
1) (4-ДВ)<d1 автокорреляция есть
2) (4-ДВ)>d1 нет
3) Д1<(4-dw)<d2 нет достаточных оснований для принятия решения
