Дана обучающая выборка 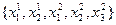 (см. Рис.1)
(см. Рис.1)
Известно, что образы 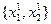
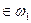 , а образы
, а образы 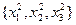
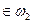
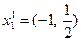
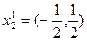
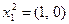
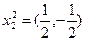
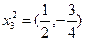

Рис. 1
Требуется по обучающей выборке построить оценки плотностей распределения.
Плотности можно аппроксимировать, применив выражения вида:
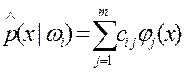
Базисные функции  считаются ортогональными в области определения образов. Поскольку наши образы
считаются ортогональными в области определения образов. Поскольку наши образы 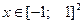 , будем использовать многочлены Лежандра, так как областью их ортогональности является интервал
, будем использовать многочлены Лежандра, так как областью их ортогональности является интервал 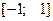 .
.
В одномерном случае эти функции определяются следующим рекуррентным соотношением:
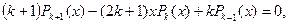
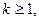
Первые члены функции P(x) имеют следующий вид:
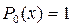 и
и 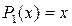
Все эти функции ортогональны. Ортонормированные функции определяются следующим выражением:
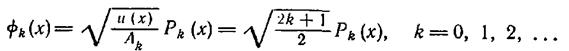
В иллюстративных целях с ортогональными функциями мы будем обращаться так, как если бы они были ортонормированными.
Множество ортогональных функций для двумерного случая легко получить, формируя произвольные попарные комбинации одномерных функций.
Пусть m=4.
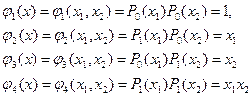
где x1,x2 – компоненты образа x.
Очевидно, что порядок формирования этих функций не единственный. Для получения любой функции 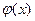 можно использовать произвольную парную комбинацию функций одной переменной.
можно использовать произвольную парную комбинацию функций одной переменной.
Теперь определим коэффициенты 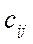 разложения
разложения 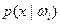 . Используя допущение ортонормированности функций, эти коэффициенты можно вычислить по формуле:
. Используя допущение ортонормированности функций, эти коэффициенты можно вычислить по формуле:
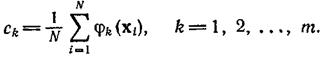
Для класса 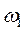 :
:
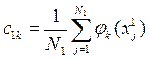
N1- число образов, входящих в класс 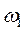 ,
, 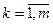
Для образов класса 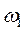 , применение данной процедуры дает
, применение данной процедуры дает
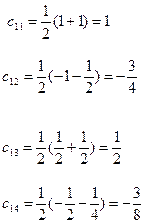 | |||
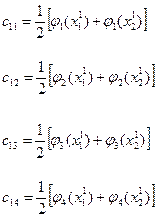 | |||
 Аналогично, для образов класса
Аналогично, для образов класса 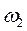 получим:
получим:
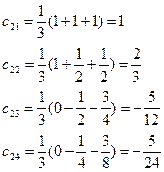
Аппроксимация плотности распределения 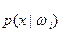 такова
такова
Аппроксимация плотности распределения 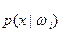 такова:
такова:
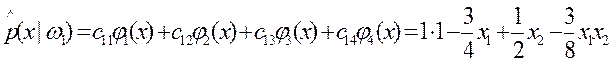
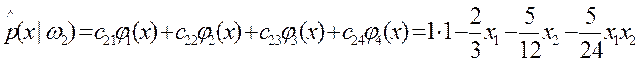
 2015-05-18
2015-05-18 372
372







