В силу неизвестности значений параметров регрессии неизвестными будут также и истинные значения отклонений 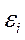 , поэтому выводы об их независимости осуществляются на основе оценок
, поэтому выводы об их независимости осуществляются на основе оценок 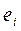 , полученных из эмпирического уравнения регрессии. Рассмотрим возможные методы определения автокорреляции.
, полученных из эмпирического уравнения регрессии. Рассмотрим возможные методы определения автокорреляции.
Графический метод. Существует несколько вариантов графического определения автокорреляции. Один из них состоит в анализе последовательно-временных графиков. По оси абсцисс откладывают время, либо порядковый номер наблюдения, а по оси ординат – отклонения 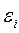 (Рис. 1).
(Рис. 1).
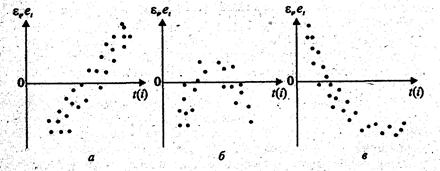
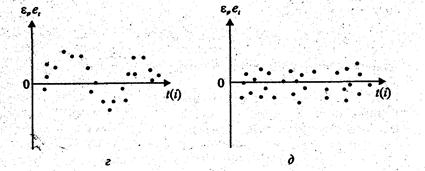
Рис. 1.
Естественно предположить, что на рис. 1, а - г имеются определенные связи между отклонениями, т.е. автокорреляция имеет место. Отсутствие зависимости на рис. 1, д скорее всего свидетельствует об отсутствии автокорреляции.
Например, на рис. 1, б отклонения вначале в основном отрицательные, затем положительные, потом снова отрицательные. Это свидетельствует о наличии между отклонениями определенной зависимости. Более того, можно утверждать, что в этом случае имеет место положительная автокорреляция остатков. Она становится весьма наглядной, если график 1, б дополнить графиком зависимости 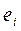 от
от 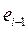 (рис. 2).
(рис. 2).
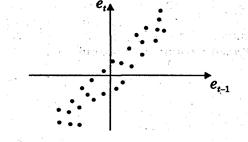
Рис. 2
Подавляющее большинство точек на этом графике расположено в I и III четвертях декартовой системы координат, подтверждая положительную зависимость между соседними отклонениями.
Современные ППП решение задач построения регрессии дополняют графическим представлением результатов: график реальных колебаний зависимой переменной накладывается на график колебаний переменной по уравнению регрессии. Сопоставление этих графиков часто дает возможность выдвинуть гипотезу о наличии автокорреляции.
Метод рядов. Последовательно определяются знаки отклонений 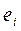 . Например,
. Например,
(-----)(+++++++)(---)(++++)(-), т.е. 5 «-», 7 «+», 3 «-», 4 «+», 1 «-» при 20 наблюдениях.
Ряд определяется как непрерывная последовательность одинаковых знаков. Количество знаков в ряду называют длиной ряда. Визуальное распределение знаков свидетельствует о неслучайном характере связей между отклонениями. Если рядов слишком мало по сравнению с количеством наблюдений n, то вполне вероятна положительная автокорреляция. Если рядов слишком много, то вероятна отрицательная автокорреляция. Пусть n – объем выборки, n1 и n2 – общее количество, соответственно, знаков «+» и «-», k – количество рядов.
При достаточно большом количестве наблюдений (n1 > 10,
n2 > 10) и отсутствии автокорреляции случайная величина k имеет асимптотически нормальное распределение с
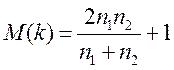 ;
; 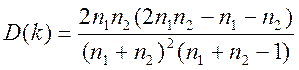 .
.
Тогда, если 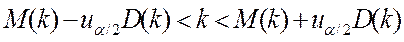 , то гипотеза об отсутствии автокорреляции не отклоняется.
, то гипотеза об отсутствии автокорреляции не отклоняется.
Число 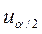 определяется по таблице функции стандартного нормального распределения из равенства F(
определяется по таблице функции стандартного нормального распределения из равенства F(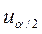 ) =
) =  . Например, при
. Например, при 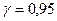 ,
, 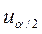 =1,96 и при
=1,96 и при 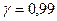 ,
, 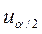 =2,58.
=2,58.
Для небольшого числа наблюдений (n1 < 20, n2 < 20) разработаны таблицы критических значений количества рядов при n наблюдениях. Суть таблиц в следующем.
На пересечении строки n1 и столбца n2 определяются нижнее k1 и верхнее k2 значения при уровне значимости 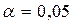 (Рис.3).
(Рис.3).
автокорреляция > 0 автокорреляция = 0 автокорреляция < 0
______k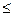 k1_________k1<k<k2_________k
k1_________k1<k<k2_________k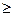 k2____________
k2____________
k1 k2
Рис.3.
Пример 1. Пусть изучается зависимость среднедушевых расходов на конечное потребление y от среднедушевого дохода х по данным некоторой страны за 16 лет.
Исходные 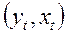 (и расчетные
(и расчетные 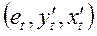 для примера 3) данные (усл.ед.) представлены в следующей таблице:
для примера 3) данные (усл.ед.) представлены в следующей таблице:
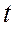 | 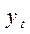 | 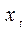 | 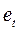 | 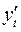 | 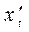 |
| 0,18 | - | - | |||
| 0,76 | 37,51 | 38,99 | |||
| 0,12 | 40,99 | 44,47 | |||
| 0,28 | 43,45 | 46,92 | |||
| -1,55 | 43,92 | 49,88 | |||
| -2,58 | 45,4 | 51,83 | |||
| -1,22 | 50,88 | 56,3 | |||
| -2,03 | 47,33 | 53,75 | |||
| 0,94 | 54,33 | 58,24 | |||
| 2,1 | 56,78 | 61,71 | |||
| 3,49 | 56,74 | 60,66 | |||
| 4,69 | 57,22 | 60,65 | |||
| -1,56 | 57,2 | 69,14 | |||
| -1,79 | 59,7 | 68,58 | |||
| -1,01 | 62,17 | 70,55 | |||
| -0,82 | 61,15 | 69,53 |
Пусть исходная модель имеет вид: 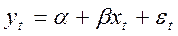 .
.
По исходным данным с использованием МНК получено следующее оцененное уравнение регрессии:
| ВЫВОД ИТОГОВ | ||||||
| Регрессионная статистика | ||||||
| Множественный R | 0,993402 | |||||
| R-квадрат | 0,986847 | |||||
| Нормированный R-квадрат | 0,985908 | |||||
| Стандартная ошибка | 2,108545 | |||||
| Наблюдения | ||||||
| Дисперсионный анализ | ||||||
| df | SS | MS | F | Значимость F | ||
| Регрессия | 4670,194 | 4670,194 | 1050,435 | 1,43E-14 | ||
| Остаток | 62,24347 | 4,445962 | ||||
| Итого | 4732,438 | |||||
| Коэффициенты | Стандартная ошибка | t-статистика | P-Значение | Нижние 95% | Верхние 95% | |
| Y-пересечение | 10,987 | 2,771947 | 3,963639 | 0,001413 | 5,041761 | 16,93223 |
| x | 0,805944 | 0,024867 | 32,41042 | 1,43E-14 | 0,75261 | 0,859278 |
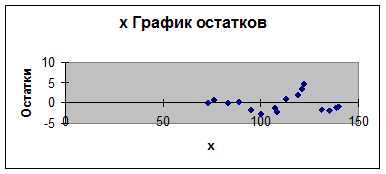
График остатков свидетельствует о наличии автокорреляции.
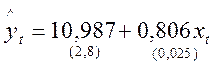 ,
, 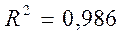
(в скобках указаны стандартные ошибки).
Используя метод рядов, получим: n = 16, (++++)(----)(++++)(----), n1 = 8 < 20, n2 = 8 < 20, k = 4. По таблицам (Приложение 1) k1 =4, k2 =14. Т.к. k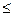 k1, то принимается предположение о наличии положительной автокорреляции (Рис. 3).
k1, то принимается предположение о наличии положительной автокорреляции (Рис. 3).
Оценкой коэффициента корреляции 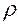 является коэффициент автокорреляции остатков первого порядка, который при достаточно большом числе наблюдений имеет вид:
является коэффициент автокорреляции остатков первого порядка, который при достаточно большом числе наблюдений имеет вид:
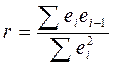 .
.
Считается, что 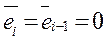 ,
, 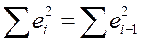 .
.
Выдвигается нулевая гипотеза об отсутствии корреляции первого порядка, т.е. 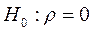 . В качестве альтернативной гипотезы может выступать либо
. В качестве альтернативной гипотезы может выступать либо 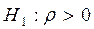 , либо
, либо 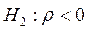 .
.
Для проверки нулевой гипотезы используют статистику Дарбина-Уотсона, рассчитываемую по формуле:
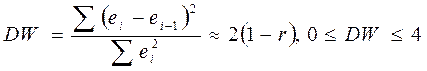 .
.
Если автокорреляция остатков отсутствует 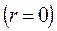 , то
, то 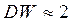 .
.
При положительной автокорреляции 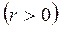 имеем
имеем  , а при отрицательной
, а при отрицательной 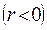 - соответственно,
- соответственно, 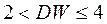 .
.
По таблице определяются критические значения критерия Дарбина-Уотсона 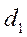 и
и 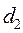 для заданного числа наблюдений, числа объясняющих переменных и уровня значимости. По этим значениям отрезок
для заданного числа наблюдений, числа объясняющих переменных и уровня значимости. По этим значениям отрезок 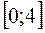 разбивается на 5 зон (рис.4). В зависимости от того, в какую зону попадает расчетное значение критерия, принимают или отвергают соответствующую гипотезу.
разбивается на 5 зон (рис.4). В зависимости от того, в какую зону попадает расчетное значение критерия, принимают или отвергают соответствующую гипотезу.
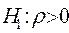 | Зона неопределенности | 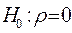 | Зона неопределенности | 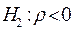 | |||||
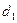 | 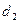 | 4-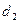 4- 4-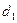 | |||||||
Рис. 4
Наличие зоны неопределенности связано с тем, что распределение DW- статистики зависит не только от числа наблюдений и числа объясняющих переменных, но и от значений объясняющих переменных.
Пример 2. Пусть оценена парная регрессия (пример 1). Рассчитаем DW – статистику: DW= 0,991. Зададим уровень значимости 5% и найдем по таблице (Приложение 2) 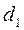 =1,106 и
=1,106 и 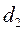 =1,371. Поскольку
=1,371. Поскольку 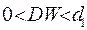 , то нулевая гипотеза отклоняется и принимается гипотеза
, то нулевая гипотеза отклоняется и принимается гипотеза 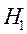 о положительной автокорреляции остатков (Рис. 4).
о положительной автокорреляции остатков (Рис. 4).
Замечание. Тест Дарбина-Уотсона разработан в предположении, что объясняющие переменные некоррелированы со случайным членом.
Обнаружение автокорреляции в модели с лаговой зависимой переменной.
Статистика Дарбина-Уотсона неприменима, когда уравнение регрессии включает лаговую зависимую переменную, например  . В таком случае можно использовать h-статистику Дарбина, которая также вычисляется на основе остатков:
. В таком случае можно использовать h-статистику Дарбина, которая также вычисляется на основе остатков:
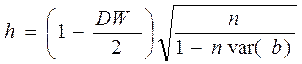 ,
,
где DW – значение статистики Дарбина-Уотсона, n – число наблюдений в выборке, var(b) – оцененная дисперсия коэффициента при лаговой зависимой переменной.
Значение h можно вычислить на основе обычных результатов оценивания регрессии. Этот тест предназначен только для проверки на наличие автокорреляции первого порядка.
При больших выборках h распределена как 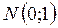 по нулевой гипотезе об отсутствии автокорреляции. Следовательно, при применении двустороннего критерия и большой выборке гипотеза об отсутствии автокорреляции может быть отклонена:
по нулевой гипотезе об отсутствии автокорреляции. Следовательно, при применении двустороннего критерия и большой выборке гипотеза об отсутствии автокорреляции может быть отклонена:
· если 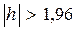 при уровне значимости 5%;
при уровне значимости 5%;
· если 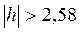 при уровне значимости 1%.
при уровне значимости 1%.
Тест Дарбина не применим, если 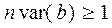 .
.
 2014-02-02
2014-02-02 2534
2534
