Четность. Закон сохранения четности и его нарушения

Инверсия, или просранственное отражение, есть изменение направления (знаков) всех трех пространственных осей координат: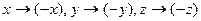

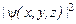определяет плотность вероятности найти микрочастицу в фиксированный м. вр. в данной точке пространства. Очевидно, что плотность вероятности не должна зависеть от того, в какой системе координат – правовинтовой (x, y, z) или левовинтовой (-x, -y, -z) выполняются наблюдения: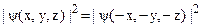

Для зеркально-симметричного процесса вероятности вылета из ядра какой-либо частицы под углам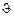и и 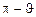относительно направления спина ядра должны быть равны. Таким образом, для зеркально симметричного процесса абсолютная величина ψ-функции не изменяется 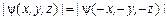(1.8.5)

О. с операция инверсии ведет к умножению ψ-функции на некоторое число Р: 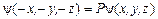(1.8.6)

Применим к выражению (1.8.6) операцию инверсии еще раз: 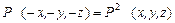где P ² 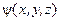должна совпадать с первоначальной функцией 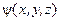. Следовательно устанавливаем, что Р ² = 1, а Р = ± 1. Величина Р называется четностью. Т.е, операция инверсии либо оставляет функцию 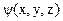неизменной, либо изменяет знак функции на обратный: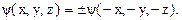

Если Р = +1, то говорят, что частица имеет положительную внутреннюю четность. Если же Р = -1, то частица имеет отрицательную внутреннюю четность. Внутренняя четность протона, нейтрона и электрона принимается положительной, т.е. для них Р = +1 Полная четность П системы, состоящей из k частиц определяется произведением полных четностей отдельных частиц: 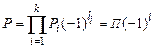(1.8.9)

Закон сохранение четности: если изолированная физическая система в момент времени t = 0 имела определенную четность, то система сохраняет свою четность во все последующие моменты времени При переходах из одного состояния в другое четность сохраняется в процессах, обусловленных сильными (с участием ядерных сил) и электромагнитными взаимодействиями. В противоположность этому в результате слабого взаимодействия (см. §3.5) четность системы не сохраняется.