Оценка значимости уравнения регрессии

Проверить значимость уравнения регрессии — значит установить, соответствует ли математическая модель, выражающая зависимость между переменными, экспериментальным данным и достаточно ли включенных в уравнение объясняющих переменных (одной или нескольких) для описания зависимой переменной. Проверка значимости уравнения регрессии производится на основе дисперсионного анализа.

Основная идея дисперсионного анализа: Q=Q_R+Q_e, (3.41) где Q – общая сумма квадратов отклонений зависимой переменной

от средней, Q_R и Q_e — соответственно сумма квадратов, обусловленная регрессией, и остаточная сумма квадратов, характеризующая влияние неучтенных факторов

Схема дисперсионного анализа:

Компоненты дисперсии	Сумма квадратов	Число степеней свободы	Средние квадраты
Регрессия		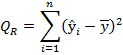m-1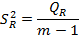
Остаточная		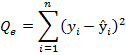n-m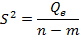
Общая		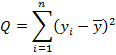n-1

Средние квадраты S_R² и S²представляют собой несмещенные оценки дисперсий зависимой переменной, обусловленных соответственно регрессий или объясняющей переменной X и воздействием неучтенных случайных факторов и ошибок; т — число оцениваемых параметров уравнения регрессии; п — число наблюдений.