2015-05-18
875
При применении регрессионного анализа на базе временных рядов в классической модели часто обнаруживается нарушение: возмущения в уравнении являются автокоррелированными.
Существует два альтернативных варианта действий при обнаружении автокорреляции:
· исследователь может попытаться изменить спецификацию модели так, чтобы устранить автокорреляцию возмущений (путем введения дополнительных признаков - регрессоров);
· выбрать такой метод оценки параметров, который при наличии автокорреляции возмущений мог бы по возможности максимально обеспечить требуемые свойства полученных оценок, например метод Эйткена.
Автокорреляция возмущений означает, что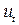 
в регрессионном уравнении для периода 
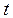зависит от возмущений более ранних периодов в том же уравнении. В простейшем случае здесь имеет место авторегрессионный процесс первого порядка.
Определение: Возмущение 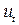подчиняется авторегрессионному процессу первого порядка, если выполняются следующие условия:
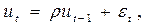где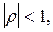 
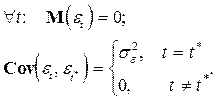(II. 1)
Замечание:
· Условие стационарности определило требование, согласно которому 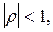что гарантирует, что влияние запаздывающего возмущения будет тем меньше, чем больше запаздывание. Таким образом, коэффициенты при 
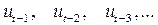соответственно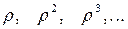 
· Случайная переменная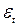 
, как специфицировано в формуле (IV. 1), свободна от автокорреляции и для всех 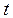имеет одинаковую дисперсию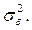 
· В случае, если условия наличия авторегрессионного процесса первого порядка выдвигаются в качестве альтернативной гипотезы, то отсутствие автокорреляции может быть записано так: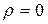 
(нулевая гипотеза).
· Авторегрессионные процессы более высокого порядка могут быть выдвинуты в качестве альтернативных гипотез, если в данных имеются циклические колебания (например, сезонные колебания в сельскохозяйственных работах имеется авторегрессия второго порядка, а в квартальных данных может наблюдаться авторегрессия четвертого порядка).
