2015-05-18
860
Ряд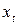 
, 
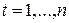, называется строго стационарным (или стационарным в узком смысле), если для любого 
(
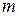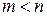) совместное распределение вероятностей случайных величин 
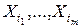такое же, как и для 
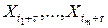, при любых 
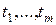и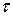 
, таких, что
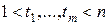и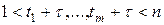 
.
Другими словами, свойства строго стационарного временного ряда не изменяются при изменении начала отсчета времени. В частности, при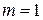 
из предположения о строгой стационарности временного ряда 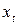следует, что закон распределения вероятностей случайной величины 
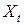не зависит от 
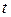, а значит, не зависят от 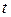и все его основные числовые характеристики (если, конечно, они существуют), в том числе: математическое ожидание 
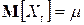E и дисперсия 
.
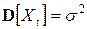Значение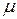 
определяет постоянный уровень, относительно которого колеблется анализируемый временной ряд 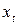, а постоянная 
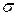характеризует размах этих колебаний.
Важно что, одно из главных отличий последовательности наблюдений, образующих временной ряд, заключается в том, что члены временного ряда являются, вообще говоря, статистически взаимозависимыми. Степень тесноты статистической связи между случайными величинам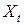и и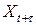 
может быть измерена парным коэффициентом корреляции
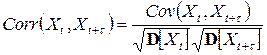
где
.
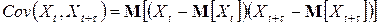Если ряд 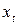стационарный, то значение 
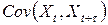не зависит от 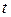и является функцией только от 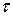; будем использовать для него обозначение 
:
.
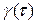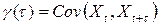В частности,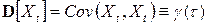 
. Соответственно, для стационарного ряда и значение коэффициента корреляции 
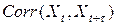зависит только от 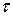; будем использовать для него обозначение 
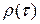,так что:
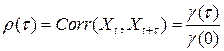
В частности,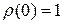 
.
Практическая проверка строгой стационарности ряда 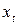на основании наблюдения значений 
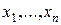в общем случае затруднительна. В связи с этим под стационарным рядом на практике часто подразумевают временной ряд 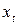, у которого:
– 
;
– 
;
– 
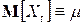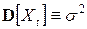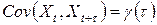для любых 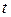и .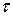
Ряд, для которого выполнены указанные три условия, называют стационарным в широком смысле (слабо стационарным, стационарным второго порядка или ковариационно стационарным) .
