2015-05-18
452
предположим, что:
– условное распределение случайного вектора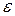 
относительно матрицы 
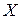является 
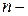мерным нормальным распределением 
;
– 
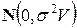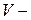известная положительно определенная матрица размерности 
.
Поскольку 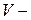ковариационная матрица, она к тому же и симметрична; таковой же будет и обратная к ней матрица 
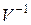. Но тогда существует такая невырожденная ()-матрица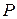 
, что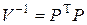 
. Используя матрицу 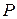, преобразуем вектор 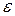к вектору: 
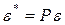. При этом 
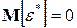и условная (относительно 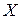)ковариационная матрица вектора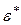 
,
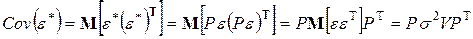так что
.
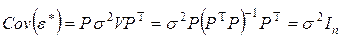Преобразуя с помощью матрицы P обе части основного уравнения
,
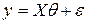получаем:
,
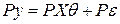или
,
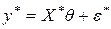где
.
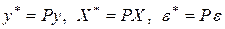В преобразованном уравнении ~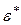 
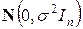, так что преобразованная модель удовлетворяет условиям, характеризующим ситуацию А'. Это означает, что все результаты, полученные в ситуации А, применимы к модели .
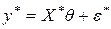В частности, оценка наименьших квадратов
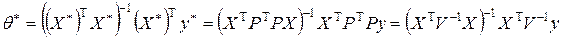
является несмещенной, т.е.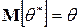 
,ее условное распределение (относительно 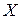)нормально и имеет ковариационную матрицу
.
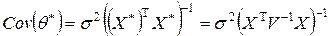Эта оценка известна как обобщенная оценка наименьших квадратов (GLS – generalized least squares) .
В рамках модели 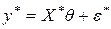можно использовать обычные статистические процедуры, основанные на 
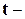и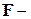 
статистиках.
Если ковариационная матрица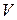 
не известна априори, то обычно ограничиваются моделями, в которых она параметризована, так что 
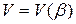,где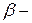 
векторный параметр, который приходится оценивать по имеющимся наблюдениям. При этом достаточно часто можно использовать стандартные выводы в асимптотическом плане, заменяя в выражении для GLS оценки 
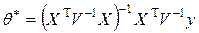неизвестную матрицу 
(
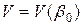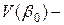истинная ковариационная матрица вектора 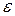)матрицей 
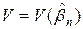,где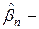 
любая состоятельная оценка для 
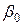. Более того, такую состоятельную оценку часто можно получить простым анализом остатков при оценивании обычной процедурой наименьших квадратов.
