Если объясняющие переменные стохастические, то в некоторых случаях все же остается возможным использовать стандартную технику статистических выводов, предназначенную для классической нормальной линейной модели, по крайней мере, в асимптотическом плане (при большом количестве наблюдений).
В этом отношении наиболее благоприятной является:
Ситуация B
– случайная величина 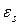 не зависит (статистически) от
не зависит (статистически) от 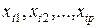 при всех
при всех 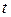 и
и 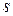 ;
;
– распределение случайной величины 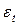 не является нормальным, но
не является нормальным, но
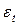 ~ i.i.d.,
~ i.i.d., 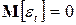 ,
, 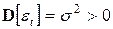 и
и 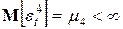 ;
;
– 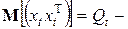 положительно определенная матрица,
положительно определенная матрица, 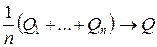 при
при 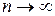 , где
, где 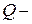 положительно определенная матрица;
положительно определенная матрица;
– 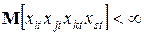 для всех
для всех 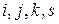 ;
;
– 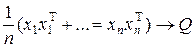 по вероятности.
по вероятности.
В силу первого предположения, оценка наименьших квадратов вектора коэффициентов 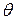 остается несмещенной, как и в ситуации A. Однако при конечном количестве наблюдений n из-за негауссовости (ненормальности) распределения
остается несмещенной, как и в ситуации A. Однако при конечном количестве наблюдений n из-за негауссовости (ненормальности) распределения 
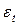 распределения статистики
распределения статистики 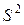 ,а также
,а также 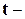 и
и 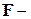 статистик, будут отличаться от стандартных, получаемых в предположении гауссовости. Чтобы продолжать пользоваться обычной техникой регрессионного анализа, необходимо сослаться на следующие асимптотические результаты, строгий вывод которых можно найти, например, в книге [Hamilton (1994)].
статистик, будут отличаться от стандартных, получаемых в предположении гауссовости. Чтобы продолжать пользоваться обычной техникой регрессионного анализа, необходимо сослаться на следующие асимптотические результаты, строгий вывод которых можно найти, например, в книге [Hamilton (1994)].
Пусть 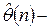 оценка наименьших квадратов вектора
оценка наименьших квадратов вектора 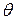 по
по 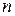 наблюдениям,
наблюдениям, 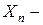 матрица значений объясняющих переменных для
матрица значений объясняющих переменных для 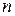 наблюдений, а
наблюдений, а 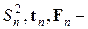 статистики
статистики 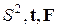 , вычисляемые по
, вычисляемые по 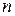 наблюдениям. Если выполнены предположения, перечисленные при описании ситуации В, то при
наблюдениям. Если выполнены предположения, перечисленные при описании ситуации В, то при 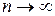
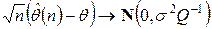 ,
,
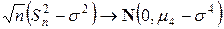 ,
,
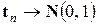 ,
,
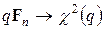 ,
,
где 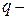 количество линейных ограничений на компоненты вектора
количество линейных ограничений на компоненты вектора 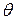 . Здесь везде имеются в виду сходимости по распределению, т.е. распределения случайных величин, стоящих слева от стрелки, неограниченно сближаются при
. Здесь везде имеются в виду сходимости по распределению, т.е. распределения случайных величин, стоящих слева от стрелки, неограниченно сближаются при 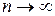 с распределениями, стоящими справа от стрелки. При этом имеют место приближенные соотношения
с распределениями, стоящими справа от стрелки. При этом имеют место приближенные соотношения
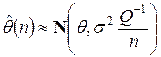 , или
, или 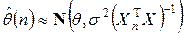 ,
,
(последнее аналогично точному соотношению в гауссовской модели),
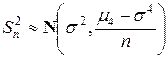 ,
,
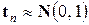 ,
,
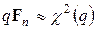 ,
,
Если в ситуации В при имеющемся количестве наблюдений 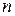 использовать не асимптотические распределения, а распределение Стьюдента
использовать не асимптотические распределения, а распределение Стьюдента 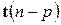 для
для 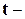 статистики (вместо
статистики (вместо 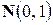 ) и распределение Фишера
) и распределение Фишера 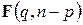 для
для 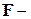 статистики (вместо
статистики (вместо 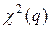 для
для 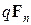 ), то это приводит к более широким доверительным интервалам (по сравнению с интервалами, построенными по асимптотическим распределениям). Многие исследователи предпочитают поступать именно таким образом, учитывая это обстоятельство и то, что при конечных п распределения Стьюдента и Фишера могут давать лучшую аппроксимацию истинных распределений статистик
), то это приводит к более широким доверительным интервалам (по сравнению с интервалами, построенными по асимптотическим распределениям). Многие исследователи предпочитают поступать именно таким образом, учитывая это обстоятельство и то, что при конечных п распределения Стьюдента и Фишера могут давать лучшую аппроксимацию истинных распределений статистик 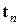 и
и 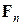 .
.
 2015-05-18
2015-05-18 400
400








