Под временным рядом (time series) понимается последовательность наблюдений значений некоторой переменной, произведенных через равные промежутки времени. Если принять длину такого промежутка за единицу времени (год, квартал, день и т.п.), то можно считать, что последовательные наблюдения 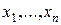 произведены в моменты
произведены в моменты 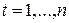 .
.
Основная отличительная особенность статистического анализа временных рядов состоит в том, что последовательность наблюдений 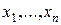 рассматривается как реализация последовательности, вообще говоря, статистически зависимых случайных величин
рассматривается как реализация последовательности, вообще говоря, статистически зависимых случайных величин 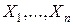 , имеющих некоторое совместное распределение с функцией распределения
, имеющих некоторое совместное распределение с функцией распределения
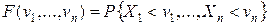 .
.
Мы будем рассматривать в основном временные ряды, у которых совместное распределение случайных величин 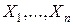 имеет совместную плотность распределения
имеет совместную плотность распределения 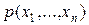 .
.
Чтобы сделать задачу статистического анализа временных рядов доступной для практического решения, приходится так или иначе ограничивать класс рассматриваемых моделей временных рядов, вводя те или иные предположения относительно структуры ряда и структуры его вероятностных характеристик. Одно из таких ограничений предполагает стационарность временного ряда.
Ряд 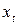 ,
, 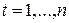 , называется строго стационарным (или стационарным в узком смысле), если для любого
, называется строго стационарным (или стационарным в узком смысле), если для любого 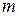 (
(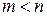 ) совместное распределение вероятностей случайных величин
) совместное распределение вероятностей случайных величин 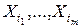 такое же, как и для
такое же, как и для 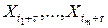 , при любых
, при любых 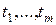 и
и 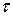 , таких, что
, таких, что
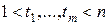 и
и 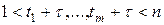 .
.
Другими словами, свойства строго стационарного временного ряда не изменяются при изменении начала отсчета времени. В частности, при 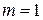 из предположения о строгой стационарности временного ряда
из предположения о строгой стационарности временного ряда 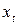 следует, что закон распределения вероятностей случайной величины
следует, что закон распределения вероятностей случайной величины 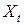 не зависит от
не зависит от 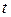 , а значит, не зависят от
, а значит, не зависят от 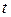 и все его основные числовые характеристики (если, конечно, они существуют), в том числе: математическое ожидание
и все его основные числовые характеристики (если, конечно, они существуют), в том числе: математическое ожидание 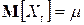 E и дисперсия
E и дисперсия 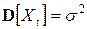 .
.
 2015-05-18
2015-05-18 553
553








