Механизм порождения последовательных наблюдений, заданный соотношениями
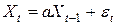 ,
, 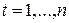 ,
,
порождает стационарный временной ряд, если:
– 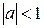 ;
;
– случайная величина 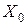 не коррелирована со случайными величинами
не коррелирована со случайными величинами 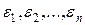 ;
;
– 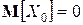 ;
;
– 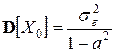 .
.
При этом 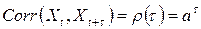 .
.
Рассмотренная модель порождает (при указанных условиях) стационарный ряд, имеющий нулевое математическое ожидание.
Без ограничения общности можно обойтись в текущем рассмотрении моделями авторегрессии, порождающими стационарный процесс с нулевым средним.
Продолжая рассмотрение для ранее определенного процесса 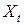 (с нулевым математическим ожиданием), заметим, что для него
(с нулевым математическим ожиданием), заметим, что для него
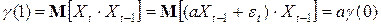 ,
,
так что: 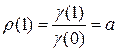 , и при значениях
, и при значениях 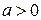 , близких к 1, между соседними наблюдениями имеется сильная положительная корреляция, что обеспечивает более гладкий характер поведения траекторий ряда по сравнению с процессом белого шума. При
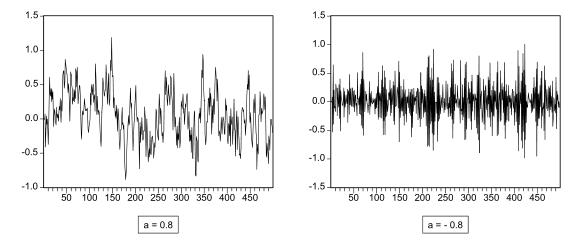
, близких к 1, между соседними наблюдениями имеется сильная положительная корреляция, что обеспечивает более гладкий характер поведения траекторий ряда по сравнению с процессом белого шума. При 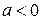 процесс авторегрессии, напротив, имеет менее гладкие реализации, поскольку в этом случае проявляется тенденция чередования знаков последовательных наблюдений. Следующие два графика демонстрируют поведение смоделированных реализаций временных рядов, порожденных моделями авторегрессии
процесс авторегрессии, напротив, имеет менее гладкие реализации, поскольку в этом случае проявляется тенденция чередования знаков последовательных наблюдений. Следующие два графика демонстрируют поведение смоделированных реализаций временных рядов, порожденных моделями авторегрессии 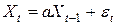 с
с 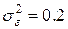 при а = 0.8 (первый график) и а = - 0.8 (второй график).
при а = 0.8 (первый график) и а = - 0.8 (второй график).
|
|
|
Далее следует обратить внимание на важное обстоятельство. В практических ситуациях «стартовое» значение 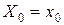 , на основе которого в соответствии с соотношением
, на основе которого в соответствии с соотношением 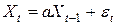 строятся последующие значения ряда
строятся последующие значения ряда 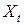 , может относиться к концу предыдущего периода, на котором просто в силу других экономических условий эволюция соответствующего экономического показателя следует иной модели, например, модели
, может относиться к концу предыдущего периода, на котором просто в силу других экономических условий эволюция соответствующего экономического показателя следует иной модели, например, модели 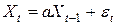 с другими значениями
с другими значениями 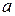 и
и 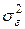 . Более того, статистические данные о поведении ряда до момента
. Более того, статистические данные о поведении ряда до момента 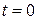 могут отсутствовать вовсе, так что значение
могут отсутствовать вовсе, так что значение 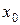 является просто некоторой наблюдаемой числовой величиной. В обоих случаях ряд
является просто некоторой наблюдаемой числовой величиной. В обоих случаях ряд 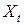 уже не будет стационарным даже при
уже не будет стационарным даже при 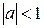 .
.
25. Ряд, порожденный моделью 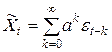 . Числовые характеристики.
. Числовые характеристики.
Механизм порождения последовательных наблюдений, заданный соотношениями
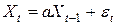 ,
, 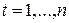 ,
,
порождает стационарный временной ряд, если:
– 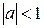 ;
;
– случайная величина 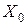 не коррелирована со случайными величинами
не коррелирована со случайными величинами 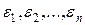 ;
;
– 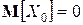 ;
;
– 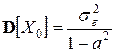 .
.
При этом 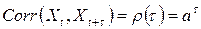 .
.
если 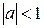 , то:
, то:
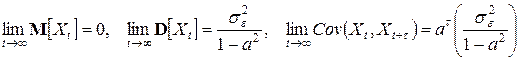 ,
,
т.е. при 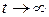 значения математического ожидания и дисперсии случайной величины
значения математического ожидания и дисперсии случайной величины 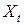 , а также автоковариации
, а также автоковариации 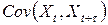 стабилизируются, приближаясь к своим предельным значениям.
стабилизируются, приближаясь к своим предельным значениям.
С этой точки зрения, условие 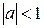 можно трактовать как условие стабильности ряда, порождаемого моделью
можно трактовать как условие стабильности ряда, порождаемого моделью 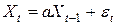 при фиксированном значении
при фиксированном значении 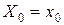 . Рассмотрим в этой ситуации наряду с только что исследованным рядом
. Рассмотрим в этой ситуации наряду с только что исследованным рядом 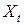 ,
,
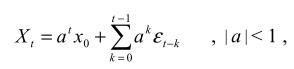
ряд, порождаемый моделью
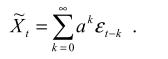
Имеем
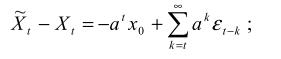
при 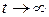

Таким образом, ряд 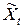 является предельным для
является предельным для 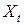 ; ряд
; ряд 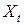 «выходит на режим»
«выходит на режим» 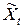 при
при 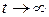 . При этом выход ряда
. При этом выход ряда 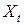 на режим
на режим 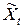 происходит тем быстрее, чем ближе
происходит тем быстрее, чем ближе 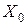 и
и 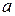 к нулю.
к нулю.
|
|
|
Для ряда 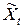
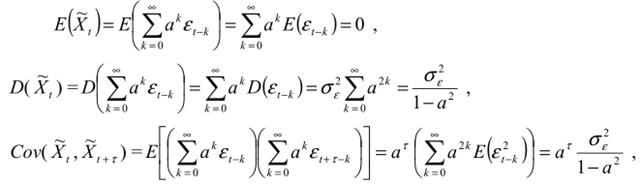
так что 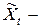 стационарный ряд (в широком смысле). Кроме того,
стационарный ряд (в широком смысле). Кроме того,
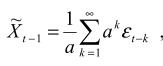
так что
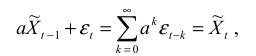
т.е. 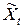 удовлетворяет соотношению
удовлетворяет соотношению
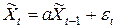 .
.
Поскольку 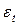 не входит в правую часть выражений для
не входит в правую часть выражений для 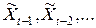 , то случайная величина
, то случайная величина 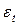 не коррелирована с
не коррелирована с 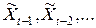 , т.е.
, т.е. 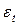 является инновацией (обновлением). В итоге получаем, что
является инновацией (обновлением). В итоге получаем, что 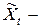 стационарный процесс авторегрессии первого порядка, и фактически именно этот процесс имеется в виду, когда говорят о стационарном процессе АR(1).
стационарный процесс авторегрессии первого порядка, и фактически именно этот процесс имеется в виду, когда говорят о стационарном процессе АR(1).
26. Процесс авторегрессии порядка 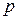 . Основные понятия и определения. Инновация. Оператор запаздывания.
. Основные понятия и определения. Инновация. Оператор запаздывания.
Модель 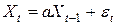 называют процессом авторегрессии первого порядка. Процесс авторегрессии порядка p (в кратком обозначении – AR(p)) определяется соотношениями
называют процессом авторегрессии первого порядка. Процесс авторегрессии порядка p (в кратком обозначении – AR(p)) определяется соотношениями
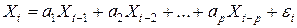 ,
, 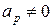 ,
,
где 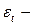 процесс белого шума с
процесс белого шума с 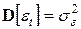 . Для простоты будем полагать, что
. Для простоты будем полагать, что 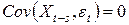 для всех
для всех 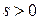 ; при этом говорят, что случайные величины
; при этом говорят, что случайные величины 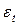 образуют инновационную (обновляющую) последовательность, а случайная величина
образуют инновационную (обновляющую) последовательность, а случайная величина 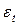 называется инновацией для наблюдения в момент
называется инновацией для наблюдения в момент 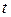 . Такая терминология объясняется тем, что наблюдаемое значение ряда в момент
. Такая терминология объясняется тем, что наблюдаемое значение ряда в момент 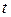 получается здесь как линейная комбинация p предшествующих значений этого ряда плюс не коррелированная с этими предшествующими значениями случайная составляющая
получается здесь как линейная комбинация p предшествующих значений этого ряда плюс не коррелированная с этими предшествующими значениями случайная составляющая 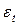 , отражающая обновленную информацию, скажем, о состоянии экономики, на момент t, влияющую на наблюдаемое значение
, отражающая обновленную информацию, скажем, о состоянии экономики, на момент t, влияющую на наблюдаемое значение 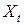 .
.
При рассмотрении процессов авторегрессии и некоторых других моделей удобно использовать оператор запаздывания L (lag operator), который воздействует на временной ряд и определяется соотношением: 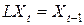 , в некоторых руководствах его называют оператором обратного сдвига и используют для него обозначение B (backshift operator).
, в некоторых руководствах его называют оператором обратного сдвига и используют для него обозначение B (backshift operator).
Если оператор запаздывания применяется k раз, что обозначается как Lk, то это дает в результате: 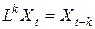 .
.
Выражение 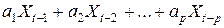 можно записать теперь в виде
можно записать теперь в виде 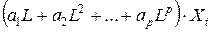 , а соотношение, определяющее процесс авторегрессии
, а соотношение, определяющее процесс авторегрессии 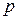 -го порядка, в виде:
-го порядка, в виде:
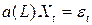
где
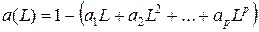 .
.
Для того, чтобы такой процесс был стационарным, все корни алгебраического уравнения: 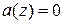 (вещественные и комплексные) должны лежать вне единичного круга
(вещественные и комплексные) должны лежать вне единичного круга 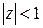 .
.
 2015-05-18
2015-05-18 642
642








