Одной из широко используемых моделей временных рядов является процесс авторегрессии (модель авторегрессии). В своей простейшей форме модель авторегрессии описывает механизм порождения ряда следующим образом:
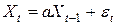 ,
, 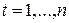 ,
,
где 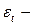 процесс белого шума, имеющий нулевое математическое ожидание и дисперсию
процесс белого шума, имеющий нулевое математическое ожидание и дисперсию 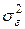 ,
, 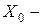 некоторая случайная величина, а
некоторая случайная величина, а 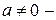 некоторый постоянный коэффициент.
некоторый постоянный коэффициент.
Механизм порождения последовательных наблюдений, заданный соотношениями
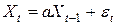 ,
, 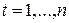 ,
,
порождает стационарный временной ряд, если:
– 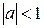 ;
;
– случайная величина 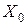 не коррелирована со случайными величинами
не коррелирована со случайными величинами 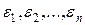 ;
;
– 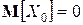 ;
;
– 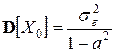 .
.
При этом 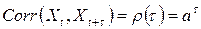 .
.
Рассмотренная модель порождает (при указанных условиях) стационарный ряд, имеющий нулевое математическое ожидание. Однако ее можно легко распространить и на временные ряды 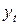 с ненулевым математическим ожиданием
с ненулевым математическим ожиданием 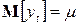 , полагая, что указанная модель относится к центрированному ряду
, полагая, что указанная модель относится к центрированному ряду 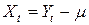 :
:
 2015-05-18
2015-05-18 563
563








