Стационарность ряда с ненулевым математическим ожиданием его элементов

Механизм порождения последовательных наблюдений, заданный соотношениями

, ,

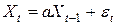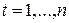порождает стационарный временной ряд, если:

– ;

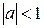– случайная величина 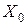не коррелирована со случайными величинами ;

– ;

– .

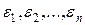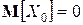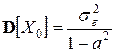При этом .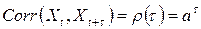

Рассмотренная модель порождает (при указанных условиях) стационарный ряд, имеющий нулевое математическое ожидание. Однако ее можно легко распространить и на временные ряды 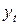с ненулевым математическим ожиданием 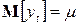, полагая, что указанная модель относится к центрированному ряду :

, ,

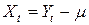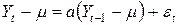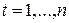так что

,

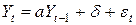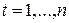
где

.

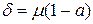Поэтому без ограничения общности можно обойтись в текущем рассмотрении моделями авторегрессии, порождающими стационарный процесс с нулевым средним.

Продолжая рассмотрение для ранее определенного процесса 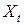(с нулевым математическим ожиданием), заметим, что для него

,

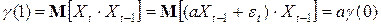так что: 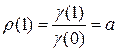, и при значениях 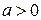, близких к 1, между соседними наблюдениями имеется сильная положительная корреляция, что обеспечивает более гладкий характер поведения траекторий ряда по сравнению с процессом белого шума. При 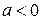процесс авторегрессии, напротив, имеет менее гладкие реализации, поскольку в этом случае проявляется тенденция чередования знаков последовательных наблюдений.