2015-05-18
2230
При рассмотрении процессов авторегрессии и некоторых других моделей удобно использовать оператор запаздывания L (lag operator), который воздействует на временной ряд и определяется соотношением: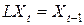 
, в некоторых руководствах его называют оператором обратного сдвига и используют для него обозначение B (backshift operator).
Если оператор запаздывания применяется k раз, что обозначается как Lk, то это дает в результате: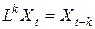 
.
Выражение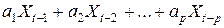 
можно записать теперь в виде 
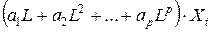, а соотношение, определяющее процесс авторегрессии 
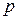-го порядка, в виде:
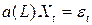
где
.
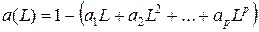Для того, чтобы такой процесс был стационарным, все корни алгебраического уравнения: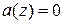 
(вещественные и комплексные) должны лежать вне единичного круга 
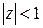. (В частности, для процесса AR(1) имеем 
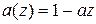, уравнение 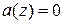имеет корень 
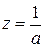, и условие стационарности 
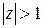равносильно уже знакомому нам условию 
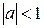) При этом решение уравнения 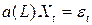можно представить в ви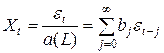де
, где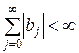 
.
откуда, в частности, следует, что
.
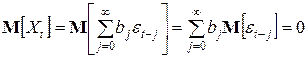Для процесса AR(1) имеем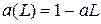 
, так что (вне зависимости от того, равно 
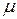нулю или нет)
.
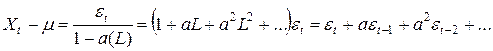Из последнего выражения сразу видно, что
.
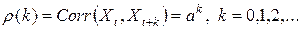28. Стационарный процесс AR(р) с нулевым математическим ожиданием.
При рассмотрении процессов авторегрессии и некоторых других моделей удобно использовать оператор запаздывания L (lag operator), который воздействует на временной ряд и определяется соотношением: 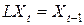, в некоторых руководствах его называют оператором обратного сдвига и используют для него обозначение B (backshift operator).
Если оператор запаздывания применяется k раз, что обозначается как Lk, то это дает в результате: .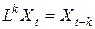
Выражение 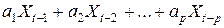можно записать теперь в виде 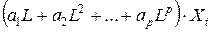, а соотношение, определяющее процесс авторегрессии 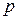-го порядка, в виде:
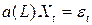
где
.
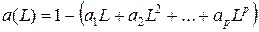Стационарный процесс AR(р) с ненулевым математическим ожиданием 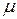удовлетворяет соотношению 
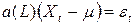, или 
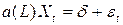, где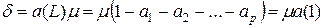 
. При этом решение уравнения 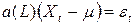имеет вид 
.
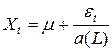Таким образом, если стационарный процесс AR(р) задан в виде 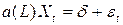, то следует помнить о том, что в этом случае математическое ожидание этого процесса равно не 
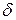, а
.
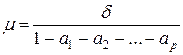Для процесса AR(1) имеем 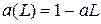, так что (вне зависимости от того, равно 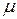нулю или нет)
.
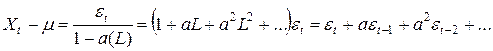Из последнего выражения сразу видно, что
.
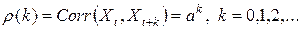При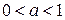 
коррелограмм (график функции 
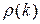для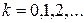 
) отражает показательное убывание корреляций с возрастанием интервала между наблюдениями; при 
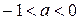коррелограмм имеет характер затухающей косинусоиды.
29. Корреляция, коррелограмм в AR(р). Система уравнений Юла-Уокера.
.
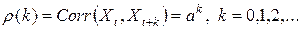При 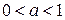коррелограмм (график функции 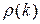для 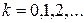) отражает показательное убывание корреляций с возрастанием интервала между наблюдениями; при 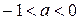коррелограмм имеет характер затухающей косинусоиды.
Коррелограмм процесса AR(р) при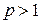 
имеет более сложную форму, зависящую от расположения (на комплексной плоскости) корней уравнения 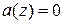. Однако для больших значений 
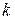автокорреляция 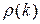хорошо аппроксимируется значением 
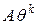, где 
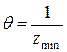и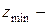 
наименьший по абсолютной величине корень уравнения 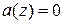, если этот корень является вещественным и положительным, или заключена в интервале 
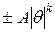в противном случае. Здесь 
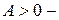некоторая постоянная, определяемая коэффициентами 
.
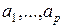Если умножить на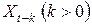 
обе части соотношения, определяющего процесс AR(р), и после этого взять от обеих частей математическое ожидание, то получим соотношение
/
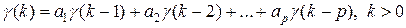Разделив обе части последнего на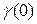 
, приходим к системе уравнений Юла-Уокера
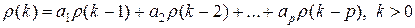
Эта система позволяет последовательно находить значения автокорреляций и дает возможность, используя первые 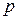уравнений, выразить коэффициенты 
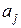через значения первых р автокорреляций, что можно непосредственно использовать при подборе модели авторегрессии к реальным статистическим данным.
[1] При имеем случай простой регрессии, а при регрессия множественная.
[2] Непременное условие: длина рядов должна быть больше количества регрессоров
\
