Процесс авторегрессии. Математическое ожидание и дисперсия

Одной из широко используемых моделей временных рядов является процесс авторегрессии (модель авторегрессии). В своей простейшей форме модель авторегрессии описывает механизм порождения ряда следующим образом:

, ,

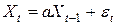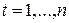где 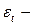процесс белого шума, имеющий нулевое математическое ожидание и дисперсию 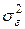, 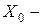некоторая случайная величина, а 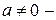некоторый постоянный коэффициент.

При этом

,

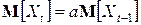так что рассматриваемый процесс может быть стационарным только если 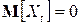для всех .

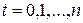Далее,

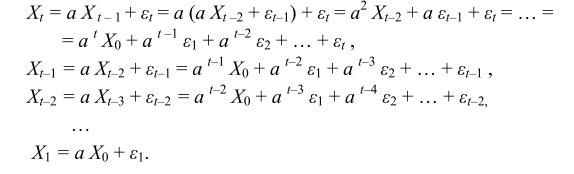
Если случайная величина 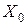не коррелирована со случайными величинами 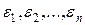, то отсюда следует, что

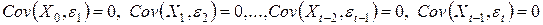
и

, .

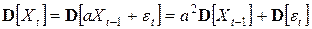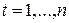Предполагая, наконец, что 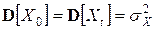для всех 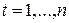, находим: 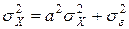, что может выполняться только при выполнении условия 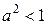, т.е. .

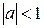При этом получаем выражение для : .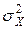

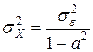Что касается автоковариаций и автокорреляций, то

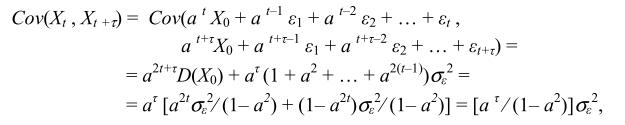
и

,

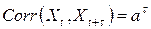т.е. при сделанных предположениях автоковариации и автокорреляции зависят только от того, насколько разнесены по времени соответствующие наблюдения.