2015-05-18
1734
По 28 предприятиям концерна изучается зависимость дневной выработки (ед.) у от уровня механизации труда (%) х по следующим данным (табл. 8).
Таблица 8
| i | x | y | i | x | y | i | x | y |
Задания:
1. Проверьте гипотезу об отсутствии гетероскедастичности в линейной регрессии с помощью теста ранговой корреляции Спирмэна при вероятности 0,95.
2. С помощью теста Гольдфельда-Квандта исследуйте гетероскедастичность остатков.
Решение:
Тест ранговой корреляции Спирмэна
Проранжируем значения хi и абсолютные величины остатков в порядке возрастания, расчеты занесем в табл. 9.
Найдем коэффициент ранговой корреляции Спирмэна:
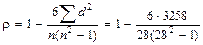= 0,108.
Таблица 9
| N | X | Ei | Расчет ранговой корреляции | |||
| Ранг Х | Ранг |Ei| | d | d^2 | |||
| 13,27 | -27 | |||||
| 7,61 | -24 | |||||
| -5,71 | -20 | |||||
| -5,67 | -18 | |||||
| -1,15 | -1 | |||||
| -2,15 | -3 | |||||
| -0,63 | ||||||
| -2,11 | ||||||
| 2,15 | -1 | |||||
| 0,41 | ||||||
| 0,67 | ||||||
| -2,03 | ||||||
| -2,77 | ||||||
| -2,51 | ||||||
| -3,25 | -2 | |||||
| -2,99 | ||||||
| -4,47 | -2 | |||||
| -5,43 | -2 | |||||
| -2,91 | ||||||
| -3,13 | ||||||
| -3,87 | ||||||
| 2,17 | ||||||
| -0,31 | ||||||
| -1,01 | ||||||
| 5,77 | ||||||
| 5,55 | ||||||
| 6,07 | ||||||
| 8,11 | ||||||
| Сумма | 0,00 |
Найдем t -критерий для ранговой корреляции:
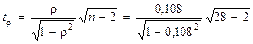= 0,556.
Сравним полученное значение t r с табличным значением
t 0,95; 26 = 2,06. Так как t r < t 0,95; 26, то на уровне значимости 5% принимается гипотеза об отсутствии гетероскедастичности.
Тест Голфреда-Квандта
Упорядочим п наблюдений по мере возрастания переменной х. Исключим из рассмотрения С = 6 центральных наблюдений (условие
(п - С)/2 = (28 – 6)/2 = 11 > р = 1 выполняется). Разделим совокупность из (п - С) = (28 – 6) = 22 наблюдений на две группы (соответственно с малыми и большими значениями фактора х по 11 наблюдений) и определим по каждой из групп уравнения регрессии. Для первой группы оно составит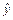 
= -3,70 + 0,39 x. Для второй группы: 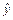= 1,16 + 53,11 x. Определим остаточные суммы квадратов для первой (S 1) и второй (S 2) групп. Промежуточные расчеты занесем в табл. 10.
Таблица 10
| N | X | Y | Yрег = -3,70 + 0,39Х | e=Y-Yрег | e^2 |
| 2,15 | 2,85 | 8,1225 | |||
| 5,66 | 0,34 | 0,1156 | |||
| 12,68 | -6,68 | 44,6224 | |||
| 14,24 | -5,24 | 27,4576 | |||
| 15,02 | -0,02 | 0,0004 | |||
| 15,02 | -1,02 | 1,0404 | |||
| 15,8 | 1,2 | 1,44 | |||
| 16,58 | 0,42 | 0,1764 | |||
| 16,97 | 5,03 | 25,3009 | |||
| 17,36 | 3,64 | 13,2496 | |||
| S1 | 121,5258 | ||||
| N | X | Y | Yрег = -53,11 + 1,16Х | e=Y-Yрег | e^2 |
| 23,45 | 1,55 | 2,4025 | |||
| 28,09 | -1,09 | 1,1881 | |||
| 30,41 | 0,59 | 0,3481 | |||
| 33,89 | -0,89 | 0,7921 | |||
| 35,05 | -2,05 | 4,2025 | |||
| 39,69 | 2,31 | 5,3361 | |||
| 42,01 | -1,01 | 1,0201 | |||
| 47,81 | -3,81 | 14,5161 | |||
| 51,29 | 1,71 | 2,9241 | |||
| 54,77 | 0,23 | 0,0529 | |||
| 57,09 | -0,09 | 0,0081 | |||
| 61,73 | 0,27 | 0,0729 | |||
| S2 | 32,8636 |
Найдем отношение R = S 1/ S 2, где S 1 > S 2.
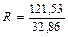= 3,69.
Сравним эту величину с табличным значением F -критерия с числом степеней свободы 8 для каждой остаточной суммы квадратов
F 0,05;8;8 = 3,44. Так как R > F 0,05;8,8, делаем вывод о наличие гетероскедастичности остатков.
