В случае парной линейной регрессии функция показателя наклона β аналогична функции коэффициента корреляции. Поэтому нужно ограничиться только одной проверкой.
H0: β = 0, то есть между переменными x, y отсутствует линейная связь в генеральной совокупности.
H1: β ≠ 0, то есть между переменными x, y есть линейная связь в генеральной совокупности.
Задается доверительная вероятность p. п — объем парной выборки. Проведем двустороннюю проверку. В этом случае а = (1 — р)/2. По таблице t -распределения находим tα ; n-2. Граничные точки ± tα ; n-2 .
Дисперсия распределения остатков вдоль линии регрессии 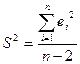 , S – стандартная ошибка.
, S – стандартная ошибка.
Стандартная ошибка коэффициента b:
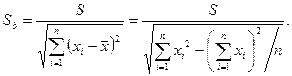
Статистика t = b/Sb.
Пример 5. Вернемся к примерам 1, 2. Проверим гипотезу о наличии линейной связи между переменными x, у в генеральной совокупности. Доверительная вероятность p = 95%. n = 5.
H0: β = 0, то есть между переменными x, y отсутствует линейная связь в генеральной совокупности.
H1: β ≠ 0, то есть между переменными x, y есть линейная связь в генеральной совокупности.
|
|
|
Проведем двустороннюю проверку.
α = (1 – р)/2 = (1 – 0,95)/2 = 0,025.
По таблице t -распределения находим tα ; n-2 = t0,025 ; 5-2 = 3,182. Граничные точки ±3,182.
| Номер | ei | ei2 |
| -0,09 | 0,0081 | |
| 0,12 | 0,0144 | |
| 0,03 | 0,0009 | |
| -0,06 | 0,0036 | |
| Сумма | 0,0270 |
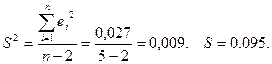
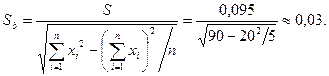
Статистика t = b/Sb = -0,11/0,03 ≈ 3,667.
Отметим значения на числовой оси.
H0 H1   2,5% 2,5% | H0  95 % 95 % | H0 H1 2,5% |
| -3,667 | -3,182 | 3,182 |
Мы отклоняем гипотезу H 0 и принимаем гипотезу H 1на уровне значимости 5%. Между переменными x, y есть линейная связь в генеральной совокупности.
Замечание. Для расчета стандартной ошибки вместо формулы 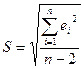 можно воспользоваться статистической функцией СТОШУХ (изв_знач_ y; изв_знач_ x) мастера функций fx пакета Excel.
можно воспользоваться статистической функцией СТОШУХ (изв_знач_ y; изв_знач_ x) мастера функций fx пакета Excel.
 2015-05-18
2015-05-18 1168
1168
