Первое уравнение системы (4.5.3) можно преобразовать к виду

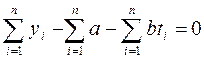
или

.

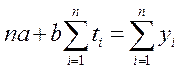Второе уравнение можно преобразовать к виду

.

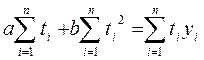Таким образом, мы имеем систему уравнений

,

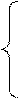
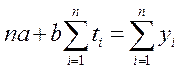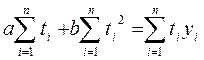. (4.5.4)

Ее решение позволяет найти оценки параметров a и b.

Для упрощения расчетов (при нечетном количестве точек ряда – 2к+1) будем считать, что ряд образуется для моментов времени – к, -к+1, … 0, 1, 2, ….. к.

Тогда

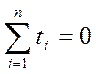
и система уравнений имеет решение

,

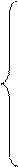
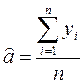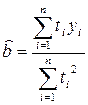. (4.5.5)

Полученная модель используется для прогноза показателя на момент времени t_L

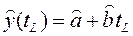(4.5.6)

Ошибки в оценке параметров приводят к ошибке в оценке тренда (среднего уровня), т. е. величина 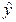(t_L) является случайной.

Дисперсия ошибки прогноза оценивается по формуле

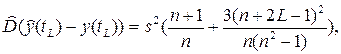(4.5.7)

где y(t_L) – истинное значение величины:

;

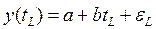n – количество точек имеющегося временного ряда;

L – количество точек периода упреждения;

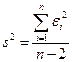- оценка остаточной дисперсии.

Из формулы (4.5.7) следует, что дисперсия ошибки прогноза увеличивается с увеличением периода упреждения (L) и уменьшается с увеличением числа точек временного ряда (n).

ПРИМЕР. Опишем динамику добычи угля в Англии за ряд лет (табл. 4.2) линейной зависимостью.

Таблица 4.2

ti	yi	ti2	yiti	ei
				-6,3
				-2,7
				2,9
				10,5
				10,0
				-1,4
				-4,8
				-7,2
				-5,6
				4,0
				1,6
				5,2
				-25,2
				19,4
Итого 105

Система уравнений (4.5.4) имеет вид

,

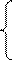
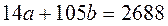
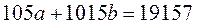откуда 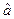=225,1; 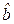= - 4,41, т. е. линейная модель имеет вид

.

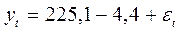При прогнозировании на 5 лет (t_L =19) прогноз добычи угля по модели составит

.

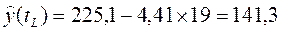Определим дисперсию ошибки прогноза по формуле (4.5.7), оценив предварительно остаточную дисперсию.

;

.

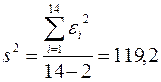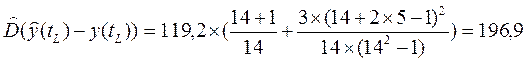Средняя квадратичная ошибка прогноза при этом составит 14,0, а коэффициент вариации

%.

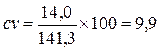Такая точность прогноза является вполне приемлемой.

4.6. ПОЛИНОМИАЛЬНЫЕ МОДЕЛИ ПРОГНОЗИРОВАНИЯ

Полиномиальная модель зависимости прогнозируемого показателя от времени имеет вид

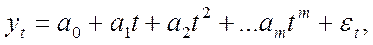(4.6.1)

где a_i – параметры модели (i=0,…,m);

t – время:

m – степень полинома.

Согласно модели (4.6.1) для фактических данных 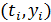(i=1,..,n) имеют место следующие соотношения

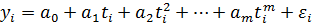(i=1,…,n).

Эти соотношения можно записать в матричном виде

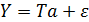, (4.6.2)

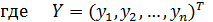– вектор-столбец значений временного ряда;

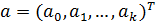– вектор-столбец значений параметров модели;

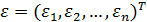- вектор-столбец случайных ошибок;

T=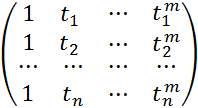

Оценки параметров а₀, a₁, … a_m можно получить с помощью рассмотренного ранее метода наименьших квадратов.

Система уравнений имеет вид

,

,

……..

.

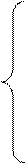
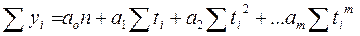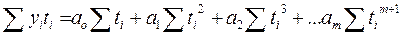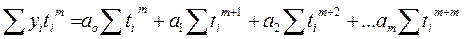Суммирование производится по индексу i от 1 до n, где n – количество точек (уровней) в динамическом ряду.

Эту систему обычно записывают в матричном виде

,

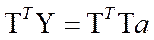где 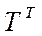- транспонированная матрица;

Отсюда

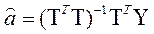. (4.6.3)

Оценки, полученные с помощью МНК, являются случайными величинами, так как представляют собой линейную комбинацию случайных величин у₁, у₂, … у_n.

Найдем математическое ожидание и дисперсию оценок параметров 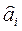(i=0,…,m). Из (4.6.2) следует, что

.

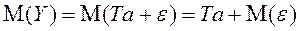Так как М(e)=0, то 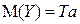и

.

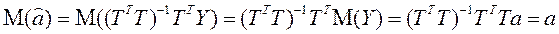Таким образом, оценки 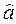являются несмещенными.