Метод проверки разности средних уровней

1. Исходный временной ряд y₁, y_2,…, y_n разбивается на две примерно равные по числу уровней части; в первой части n₁ уровней, во второй – n₂ уровней, при этом n=n₁+n₂
2. Для каждых из частей вычисляется среднее значение и дисперсия.

;

;

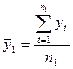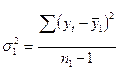
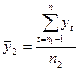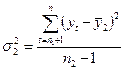
1. Проверка однородности дисперсий обеих частей ряда с помощью F-критерия Фишера.

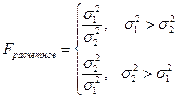
F _{расчетное} сравнивают с табличным значением с заданным уровнем значимости 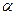( 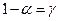- доверительная вероятность) ,

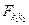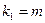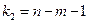, , где 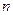- число уровней ряда, 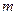- число факторов.

Например,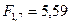

Если F _{расчетное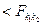} , то гипотеза о равенстве (однородности) дисперсий принимается; переходят к следующему этапу.

Если F _{расчетное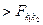} , то гипотеза о равенстве (однородности) дисперсий отклоняется, делается вывод, что данный метод для определения наличия тренда ответа не дает.

1. Проверяется гипотеза об отсутствии тренда с использованием t-критерия Стьюдента

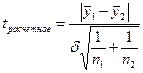
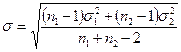-среднеквадратическое отклонение разности средних

Табличное значение: 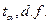, 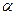(0,1; 0,05; 0,01), d.f.=n-m-1, 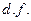-степени вероятности

Если 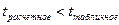, то гипотеза об отсутствии тренда принимается, т.е. тренда нет.

Если 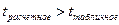, то гипотеза об отсутствии тренда отклоняется, т.е. тренд есть.