Оценка адекватности и точности трендовых моделей

Адекватность – это соответствие модели исследуемому процессу или объекту

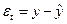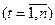, - фактические остатки

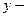исходные данные

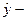теоретические (или регрессионные) данные

Модель адекватна, если выполняются все 4 свойства.

1. Проверка случайности колебаний уровней остаточной последовательности, т.е. проверка гипотезы о правильности выбора вида тренда.

Характер этих отклонений 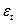изучается с помощью ряда непараметрических критериев, например критерия пиков.

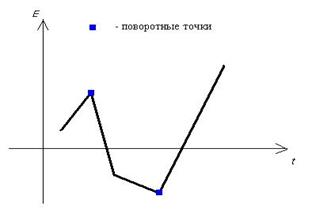
m – количество поворотных точек

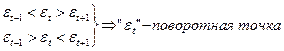
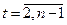
Далее m сравнивают с 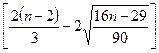, […] – целая часть, n – количество уровней

Если m > 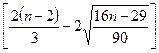, то свойство выполняется.

1. Проверка соответствия распределения случайной компоненты нормальному закону распределения с помощью R/S критерия

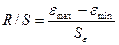
R – размах вариации

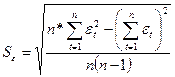- среднеквадратическая ошибка

Если 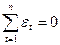, то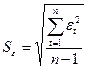

Далее расчетное значение R/S сравнивают с таблицей. Например, для n= 9 значение R/S должно попадать в интервал от 2,7 до 3,7. Если 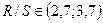, то свойство выполняется.

1. Проверка равенства математического ожидания случайной компоненты нулю с помощью t критерия Стьюдента

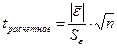
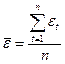
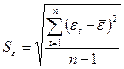
Если 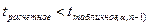, то гипотеза о равенстве математического ожидания нулю принимается, свойство выполняется.

Если 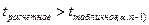, то гипотеза о равенстве математического ожидания нулю отвергается, свойство не выполняется.

1. Проверка независимости значений уровней случайной компоненты, т.е. проверка отсутствия существенной автокорреляции с помощью d критерия Дарбина-Уотсона

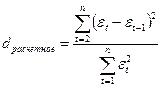
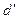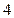
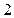
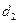
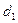
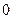
а) Если 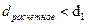, то свойство не выполняется, присутствует автокорреляция.

б) Если 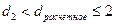, свойство выполняется, остатки независимы, отсутствует автокорреляция.

в) Если 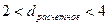, то находят d’, d’=4-d, далее смотрят, в какой интервал попадает d’.

г) Если 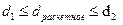, то критерий Дарбина-Уотсона ответа не дает. Применяют критерий первого коэффициента автокорреляции.

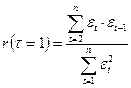
Далее расчетное значение сравнивают с табличным. При 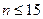r_{табличное} =0,36

Если 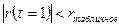, то свойство выполняется