Оценим общее качество модели.
Качество построенной модели в целом оценивает коэффициент (индекс) детерминации, который представляет собой долю дисперсии, объясненной выбранным фактором. Коэффициент детерминации R 2(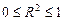 ) рассчитывается как квадрат коэффициента корреляции для парной регрессии. В Excel множественный R для парной регрессии равен коэффициенту корреляции. Скорректированный (нормированный) индекс детерминации ) рассчитывается как квадрат коэффициента корреляции для парной регрессии. В Excel множественный R для парной регрессии равен коэффициенту корреляции. Скорректированный (нормированный) индекс детерминации 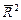 позволяет более точно определить качество модели. Если R 2 = 1, то все точки наблюдения лежат на регрессионной прямой. Для определения статистической значимости коэффициента детерминации используется F -стати- стика, рассчитываемая по формуле: позволяет более точно определить качество модели. Если R 2 = 1, то все точки наблюдения лежат на регрессионной прямой. Для определения статистической значимости коэффициента детерминации используется F -стати- стика, рассчитываемая по формуле: 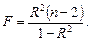 Величина F имеет распределение Фишера с v 1 = 1, v 2 = n – 2 степенями свободы. По выборке находится наблюдаемое значение Fнабл статистики. Если Fнабл Величина F имеет распределение Фишера с v 1 = 1, v 2 = n – 2 степенями свободы. По выборке находится наблюдаемое значение Fнабл статистики. Если Fнабл 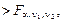 то R 2 значим ( то R 2 значим (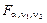 = Fкр – критическая точка распределения Фишера, зависящая только от объема выборки). = Fкр – критическая точка распределения Фишера, зависящая только от объема выборки).
|
Указанные показатели находятся в таблице «Регрессионная статистика» листа «Регрессия»(таблица 7).
Таблица 7 – Регрессионная статистика
| ВЫВОД ИТОГОВ | |
| Регрессионная статистика | |
| Множественный R | 0,99 |
| R-квадрат | 0,97 |
| Нормированный R-квадрат | 0,97 |
| Стандартная ошибка | 14,04 |
| Наблюдения |
Коэффициент множественной детерминации R-квадрат равен 0,97. Так как коэффициент множественной детерминации близок к 1, то уравнение имеет высокое качество. Этот факт подтверждает также нормированный индекс множественной детерминации, равный 0,97.
Значимость коэффициента множественной детерминации R-квадрат устанавливается с помощью критерия Фишера в таблице «Дисперсионный анализ» листа «Регрессия» (таблица 8).
Таблица 8 – Дисперсионный анализ
| Дисперсионный анализ | |||||
| df | SS | MS | F | Значимость F | |
| Регрессия | 132 547 | 132 547,02 | 672,45 | 1,04E–15 | |
| Остаток | 3 547,98 | 197,11 | |||
| Итого | 136 095 | ||||
| Fкр | 4,41 |
Так как наблюдаемое значение Fнабл = 672,45 > Fкр = 4,41, то
R-квадрат значим (значительно отличается от нуля), что еще раз подтверждает высокое качество построенного уравнения регрессии.
 2015-05-18
2015-05-18 623
623








