Задача 6. Для задачи 3 вычислить R12 и R22, сравнить, объяснить различие и выбрать лучшее уравнение регрессии

Для задачи 3 вычислить R₁² и R₂², сравнить, объяснить различие и выбрать лучшее уравнение регрессии, объяснить почему.

Ответ: R₁² = 0,96886, R₂² = 0,42433, первое уравнение лучше.

В линейной регрессии обычно оценивается значимость не только уравнения в целом, но и отдельных его параметров. С этой целью по каждому из параметров и коэффициенту регрессии определяется его стандартная ошибка: m_b и m_a, m_r

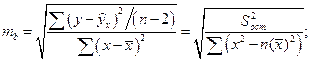
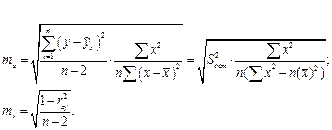
Выдвигается гипотеза 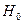о случайной природе показателей, т.е. о незначительном их отличии от нуля. Оценка значимости коэффициентов регрессии и корреляции с помощью t-критерия Стьюдента проводится путем сопоставления их значений с величиной случайной ошибки:

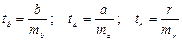
Затем сравнивая фактическое и критическое (табличное значения t-статистики) принимаем или отвергаем гипотезу .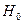

Если t_табл < t_факт, то 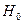отклоняется.

(Если критерий 2х сторонний: t_факт ≥ t_табл и t_факт ≤ t_табл или t_факт ≥ |t_табл|).

Для задач 1 и 4 найти критерий Стьюдента для a,b и r_xy и вычислить доверительные интервалы для коэффициентов.

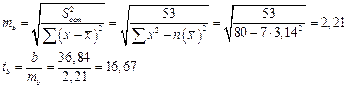
Проверка: Связь между F-критериями Фишера и t-статистикой Стьюдента

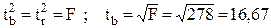
Из таблицы 2 для уровня значимости α = 0,05 и числа степеней свободы n – 2 = 5, получим t_b = 2.57. Т.к. фактически значение > табличного, то гипотезу о несущественности коэффициента регрессии ''b'' можно отклонить. Доверительный интервал для коэффициента регрессии определяется как

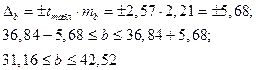
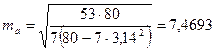
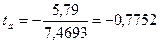t_табл.=2,57

-0,7752>-2,75, т.е. коэффициент «а» статистически не значим, т.е. Н_о не отклоняется. Доверительный интервал для «а» не определяется.

Значимость линейного коэффициента корреляции определим на основе величины ошибки m_r

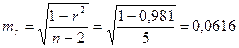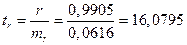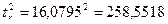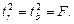; ; ; т.е.

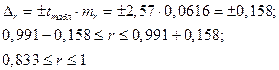
Рассмотренная формула для т_r рекомендуется к применению при большом числе наблюдений и если r не близко к +1 или -1. Если корреляция близка к +1, то распределение его оценок отличается от нормального или распределения Стьюдента, т.к. величина r_xy ограничена значениями. Р. Фишер предложил для оценки вклада r_xy ввести вспомогательную величину z, связанную с r_xy следующим отношением:

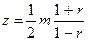
При изменении r от -1 до +1 z изменяется от 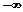до 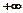, что соответствует нормальному распределению. Стандартная ошибка вычисляется по формуле

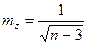, где n – число наблюдений.

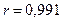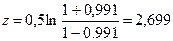В нашем примере тогда , а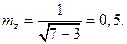

Для вычисления величины z есть таблицы z -преобразований, приложения III из [11], для числа степеней свободы 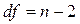и уровня значимости 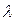даны фактические значения .

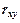Если не пользоваться таблицами, то стандартную ошибку можно определить

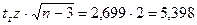
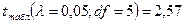
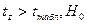отвергается, т.е.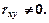

6. Стандартная ошибка уравнения регрессии. Прогнозное значение.

В прогнозных расчетах по уравнению регрессии можно определить предсказываемое значение (у_р) как точечный прогноз 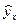при 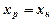, т.е. путем подстановки в уравнение регрессии 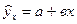соответствующего значения х. Вычислим сначала стандартную ошибку 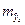, а затем интервальную оценку прогнозного значения у^*

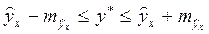
Стандартная ошибка 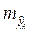зависит от ошибки 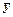и ошибки коэффициента регрессии b, т.е.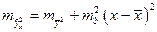

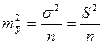; где S² остаточная дисперсия на одну степень свободы.

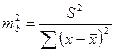
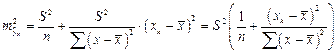
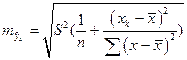
найдем при х_к=4.

;

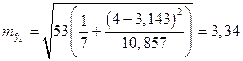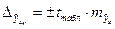
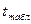-табличное значение критерия Стьюдента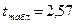

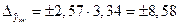
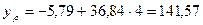- точечный прогноз.

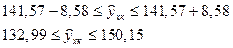
Этот доверительный интервал получился без учета случайной ошибки , если ее учитывать получим

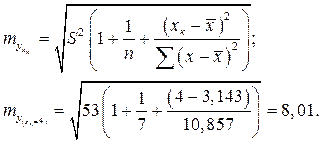
Доверительный интервал в этом случае будет

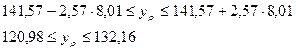
Задача 7. Наблюдения 16 пар (Х и Y) дали следующие результаты:

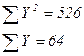
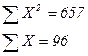
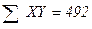
Оцените регрессию 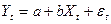и проверьте гипотезу, что коэффициент b=1,0.

1. Оценим параметры регрессии

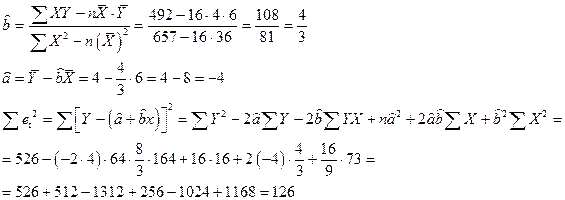
Оценка дисперсии ошибок равна

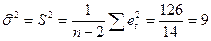
2. Проверка гипотезы Н₁: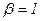

Оценка дисперсии b:

;

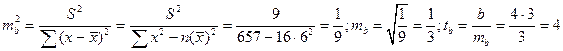Для проверки гипотезы Н₁ найдем:

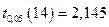, следовательно 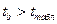, следовательно 4 > 2,145.

Поэтому Н₁: 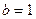не отвергаем (на уровне значимости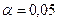 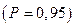) и при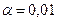 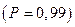тоже нет оснований отвергать гипотезу H₁, т.к. .

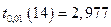Задача 8. Получена регрессионная зависимость расходов на питание от располагаемого личного дохода населения США за 25-летний срок (1959-1983 гг.). Уравнение регрессии имеет вид:

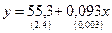
Цифры в скобках есть стандартные ошибки.

Сформулируем Н₀: b₀=0 и попытаемся ее опровергнуть

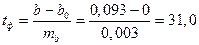
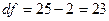, оцениваем два параметра «а» и «b».

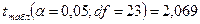
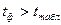; Н₀ отвергается.

Критерий можно записать в виде неравенств:

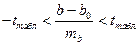
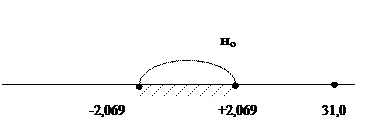
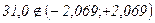, что противоречит Н₀, поэтому ее отвергаем, т.е. 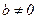, значит коэффициент «b» статистически значим.

Для параметра «а»

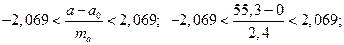
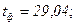
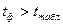
Коэффициент «а» статистически значим.

Задача 9. Модель зависимость между общей инфляцией и инфляцией, вызванной ростом заработной платы имеет вид (в скобках указаны стандартные ошибки)

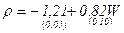
Проверить значимость коэффициентов «а» и «b», если число наблюдений 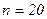, а уровень значимости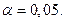

Ответ: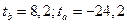

Задача 10. Уравнения регрессии между расходами на коммунальные услуги и (1) располагаемым личным доходом и (2) временем за период с 1959г. по 1983г. в США имеют вид:

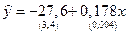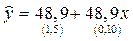(1) (2)

В скобках указаны стандартные ошибки.

Выполните t -тест для проверки значимости коэффициентов.

.