Метод наименьших квадратов. Метод наименьших квадратов относится к важному разделу организационно-экономического моделирования и прикладной статистики - многомерному статистическому

Метод наименьших квадратов относится к важному разделу организационно-экономического моделирования и прикладной статистики - многомерному статистическому анализу. В многомерном статистическом анализе исходные данные - это как минимум пара чисел (t_i, X_i) (а не одно число).

Предполагается, что переменная X линейно зависит от переменной t, т.е.

X (t) = a (t – t _ср.) + b -

Это - теоретическая модель, а практически известны исходные данные – набор пар чисел (t_i, X_i), i = 1, 2, 3, …, n, где:

t_i – независимая переменная (например, время, а в случае определения выборочной функции спроса - цена p_i),

X_i – зависимая переменная (например, индекс инфляции, курс доллара, а в случае определения выборочной функции спроса это будет спрос D (p_i)).

Предполагается, что переменные связаны линейной зависимостью:

X_i = a (t_i – t _ср.) + b + e_i , i = 1, 2, 3, …, n.

Это - реальная зависимость, учитывающая погрешности (e_i), искажающие зависимость, параметры a и b нам неизвестны и подлежат оцениванию, а

t _ср.= .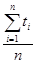

Обычно параметры a и b оценивают методом наименьших квадратов.

Согласно этому методу для расчета наилучшей функции, приближающей линейным образом зависимость X от t, следует рассмотреть функцию двух переменных:

f (a,b) = 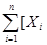- a (t_i – t _ср) – b ]².

Фактически – это есть сумма квадратов разностей между реальными значениями функции и теоретически определенными значениями функции от независимой переменной.

Оценки метода наименьших квадратов – это такие значения a и b, при которых функция f (a,b) достигает минимума по всем значениям аргументов. Чтобы найти эти оценки, надо вычислить частные производные от функции f (a,b) по аргументам a и b, т.е. 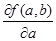и 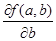, и приравнять их к 0.

Из полученных уравнений путем внутриматематических преобразований получим оценки:

,

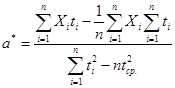
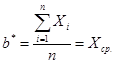
Следовательно, восстановленная функция, с помощью которой можно прогнозировать, имеет вид:

.

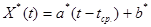Это - теоретическая функция, в которой вместо параметров подставлены их оценки, что позволяет проводить прогнозирование на какой-то интервал независимой переменной t вперед, а также интерполировать эти данные на моменты между наблюдениями.

Если взять другие обозначения, то линейная зависимость может выглядеть так:

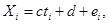i = 1, 2, 3, …., n. (1)

Сравнивая выражения:

X_i = a (t_i – t _ср.) + b +e_i = at_i – at _ср. + b +e_i

и (1), легко перейти от одного к другому:

c =a, d = b – at _ср.

Аналогичные соотношения справедливы и для оценок:

c^* = a^*, d^* = b^* -a^*t _ср,

X_i^* = c^*t_i + d^*.

Оценкой погрешности (невязки) e_i является кажущаяся невязка

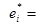X_i - X_i^*.

Возникает вопрос, насколько точно оценивается зависимость. Чтобы ответить на него, надо ввести модель порождения данных:

,

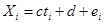где e _1, e ₂…… e_n - независимые, одинаково распределенные случайные величины с математическим ожиданием 0 и дисперсией .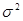

Таким образом, модель описывается тремя параметрами: c, d и 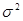. Параметры c и d мы умеем оценивать, а для оценки 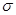² используется следующая формула:

= ,

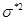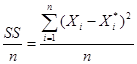где SS - так называемая остаточная сумма квадратов, 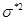- оценка дисперсии.

Доверительные интервалы для прогностической функции записываются следующим образом (см. п.3.1 главы 3 настоящего учебника):

,

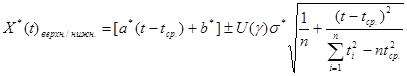
где ,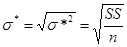

U (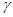) –квантиль стандартного нормального распределения порядка .

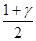При доверительной вероятности 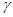= 0,95 находим из таблиц U (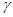) = 1,96, при 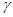= 0,99 имеем U (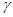) = 2,58, и U (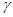) = 1,64 при 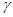= 0,9.