Будем использовать формулу: 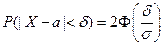 , где
, где 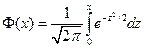 - нормированная функция Лапласа (значения берутся из таблицы). По условию также известно, что
- нормированная функция Лапласа (значения берутся из таблицы). По условию также известно, что 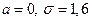 мм.
мм.
Получаем вероятность, что отклонение его диаметра от проектного размера не превышает 2 мм:
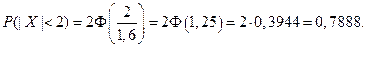
Ответ: 78,88% стандартных валиков.
ЗАДАЧА 2
В результате эксперимента получены данные, записанные в виде статистического ряда. Требуется:
1) записать значения результатов эксперимента в виде
вариационного ряда;
2) найти размах варьирования и разбить его на 9 интервалов;
3) построить полигон частот, гистограмму относительных
частот и график эмпирической функции распределения;
4) найти числовые характеристики выборки 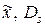 ;
;
5) приняв в качестве нулевой гипотезу 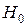 : генеральная совокупность, из которой извлечена выборка, имеет нормальное
: генеральная совокупность, из которой извлечена выборка, имеет нормальное
распределение, проверить ее, пользуясь критерием Пирсона
при уровне значимости 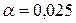 ;
;
6) найти доверительные интервалы для математического
ожидания и среднего квадратичного отклонения при надежности 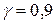
7)
| 17,1 | 21,4 | 15,9 | 19,1 | 22,4 | 20,7 | 15,1 | 18,2 | 20,3 | 16,7 | |||||||||
| 19,1 | 20,5 | 14,2 | 16,9 | 17,8 | 18,3 | 19,1 | 21,4 | 14,5 | 16,1 | |||||||||
| 16,2 | 17,3 | 22,5 | 19,9 | 21,1 | 18,5 | 17,1 | 22,4 | 20,8 | 19,8 | |||||||||
| 17.5 | 19,2 | 18.5 | 15,7 | 14,0 | 18,8 | 19,5 | 21,6 | 15,3 | 17,3 | |||||||||
| 18,8 | 14.3 | 17,1 | 19,5 | 16,3 | 15,4 | 21,3 | 14,3 | 20,5 | 16,4 | |||||||||
| 15.6 | 17,4 | 21,3 | 22,1 | 20,1 | 23,0 | 18,9 | 15,9 | 18,2 | 20,7 | |||||||||
| 16,4 | 18,7 | 14,3 | 18,2 | 19,1 | 18,4 | 17,5 | 19,3 | 22,7 | 19,6 | |||||||||
| 22,8 | 17,5 | 20,2 | 15,5 | 21,6 | 18,1 | 16,6 | 18,3 | 15,5 | 17,7 | |||||||||
| 20,8 | 16,6 | 18,3 | 21,7 | 17,4 | 17,8 | 18,5 | 14,0 | 21,9 | 16,9 | |||||||||
| 18,9 | 14,7 | 19,5 | 20,9 | 15,8 | 18,9 | 15,6 | 21,1 | 20,2 | 15,1 | |||||||||
Решение. Запишем значения результатов эксперимента в виде
вариационного ряда.
| варианта | частота |
| 14,0 | 2,0 |
| 14,2 | 1,0 |
| 14,3 | 3,0 |
| 14,5 | 1,0 |
| 14,7 | 1,0 |
| 15,1 | 2,0 |
| 15,3 | 1,0 |
| 15,4 | 1,0 |
| 15,5 | 2,0 |
| 15,6 | 2,0 |
| 15,7 | 1,0 |
| 15,8 | 1,0 |
| 15,9 | 2,0 |
| 16,1 | 1,0 |
| 16,2 | 1,0 |
| 16,3 | 1,0 |
| 16,4 | 2,0 |
| 16,6 | 2,0 |
| 16,7 | 1,0 |
| 16,9 | 2,0 |
| 17,1 | 3,0 |
| 17,3 | 2,0 |
| 17,4 | 2,0 |
| 17,5 | 3,0 |
| 17,7 | 1,0 |
| 17,8 | 2,0 |
| 18,1 | 1,0 |
| 18,2 | 3,0 |
| 18,3 | 3,0 |
| 18,4 | 1,0 |
| 18,5 | 3,0 |
| 18,7 | 1,0 |
| 18,8 | 2,0 |
| 18,9 | 3,0 |
| 19,1 | 4,0 |
| 19,2 | 1,0 |
| 19,3 | 1,0 |
| 19,5 | 3,0 |
| 19,6 | 1,0 |
| 19,8 | 1,0 |
| 19,9 | 1,0 |
| 20,1 | 1,0 |
| 20,2 | 2,0 |
| 20,3 | 1,0 |
| 20,5 | 2,0 |
| 20,7 | 2,0 |
| 20,8 | 2,0 |
| 20,9 | 1,0 |
| 21,1 | 2,0 |
| 21,3 | 2,0 |
| 21,4 | 2,0 |
| 21,6 | 2,0 |
| 21,7 | 1,0 |
| 21,9 | 1,0 |
| 22,1 | 1,0 |
| 22,4 | 2,0 |
| 22,5 | 1,0 |
| 22,7 | 1,0 |
| 22,8 | 1,0 |
| 23,0 | 1,0 |
Найдем размах варьирования 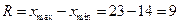 .
.
Разобьем его на 9 интервалов, длина каждого будет 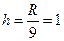 .
.
Получим интервальный ряд:
| интервал | начало | конец | частота |
| 8,0 | |||
| 12,0 | |||
| 10,0 | |||
| 13,0 | |||
| 17,0 | |||
| 12,0 | |||
| 11,0 | |||
| 10,0 | |||
| 7,0 |
Построим полигон частот:
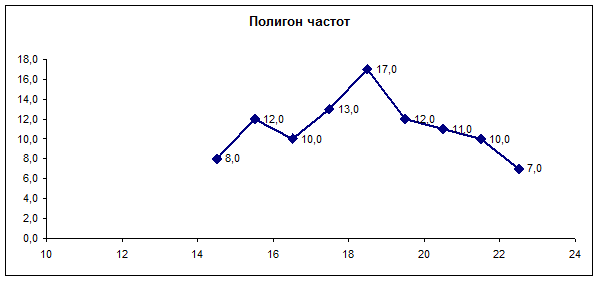
Построим гистограмму относительных частот. Вычислим относительные частоты 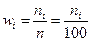 , плотности относительных частот
, плотности относительных частот 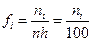 , а также накопленные относительные частоты (для следующего графика).
, а также накопленные относительные частоты (для следующего графика).
Строим гистограмму:
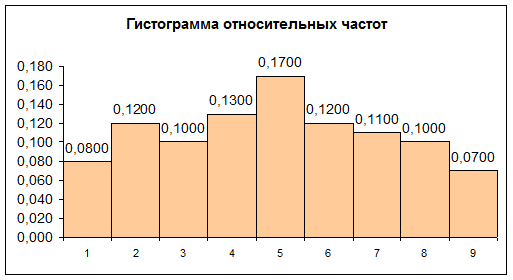
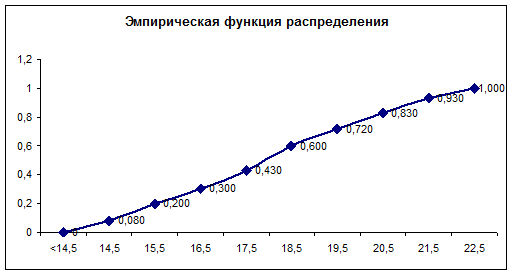
Построим график эмпирической функции распределения.
Найдем числовые характеристики выборки 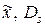 .
.
Для расчета характеристик перейдем к простому вариационному ряду, в качестве вариант выберем середины интервалов.
Выборочная средняя 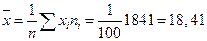 .
.
Выборочная дисперсия 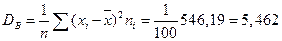
Выборочная исправленная дисперсия 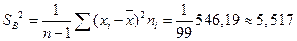
Выборочное исправленное среднеквадратическое отклонение 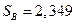
Расчеты в таблице ниже.
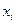 | 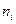 | 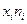 | 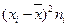 |
| 14,5 | 122,3048 | ||
| 15,5 | 101,6172 | ||
| 16,5 | 36,481 | ||
| 17,5 | 227,5 | 10,7653 | |
| 18,5 | 314,5 | 0,1377 | |
| 19,5 | 14,2572 | ||
| 20,5 | 225,5 | 48,0491 | |
| 21,5 | 95,481 | ||
| 22,5 | 157,5 | 117,0967 | |
| Сумма | 546,19 |
Примем в качестве нулевой гипотезу 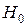 : генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение с параметрами
: генеральная совокупность, из которой извлечена выборка, имеет нормальное распределение с параметрами 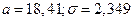 . Проверим ее, пользуясь критерием Пирсона при уровне значимости
. Проверим ее, пользуясь критерием Пирсона при уровне значимости 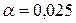 .
.
Пронормируем случайную величину 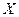 , то есть перейдем к величине
, то есть перейдем к величине 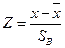 , вычислим концы интервалов по формулам
, вычислим концы интервалов по формулам 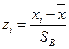 ,
, 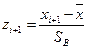 . Вычислим теоретические (гипотетические частоты)
. Вычислим теоретические (гипотетические частоты) 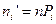 , где
, где 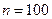 ,
, 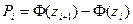 - вероятность попадания в интервал
- вероятность попадания в интервал 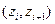 ,
, 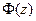 - функция Лапласа. Для нахождения значений составим расчетную таблицу:
- функция Лапласа. Для нахождения значений составим расчетную таблицу:
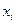 | 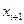 | 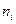 | 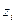 | 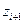 | 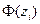 | 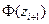 | 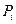 | 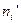 | 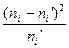 |
| -1,8775 | -1,4518 | -0,5000 | -0,4267 | 0,0733 | 7,3282 | 0,0616 | |||
| -1,4518 | -1,0260 | -0,4267 | -0,3476 | 0,0792 | 7,9155 | 2,1076 | |||
| -1,0260 | -0,6003 | -0,3476 | -0,2258 | 0,1217 | 12,1718 | 0,3875 | |||
| -0,6003 | -0,1746 | -0,2258 | -0,0693 | 0,1566 | 15,6560 | 0,4506 | |||
| -0,1746 | 0,2512 | -0,0693 | 0,0992 | 0,1685 | 16,8450 | 0,0014 | |||
| 0,2512 | 0,6769 | 0,0992 | 0,2508 | 0,1516 | 15,1609 | 0,659 | |||
| 0,6769 | 1,1027 | 0,2508 | 0,3649 | 0,1141 | 11,4140 | 0,015 | |||
| 1,1027 | 1,5284 | 0,3649 | 0,4368 | 0,0719 | 7,1880 | 1,1001 | |||
| 1,5284 | 1,9542 | 0,4368 | 0,4747 | 0,0379 | 3,7864 | 2,7275 | |||
| Сумма | 7,5103 |
Наблюдаемое значение критерия вычислим по формуле
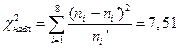 .
.
По таблице критических значений 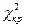 при уровне значимости
при уровне значимости 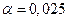 и числе степеней свободы
и числе степеней свободы 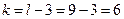 найдем
найдем 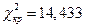 . Так как
. Так как 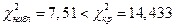 , можно принять нулевую гипотезу о нормальном распределении при данном уровне значимости.
, можно принять нулевую гипотезу о нормальном распределении при данном уровне значимости.
Найдем доверительные интервалы для математического ожидания М(Х) и среднего квадратичного отклонения σ(Х) при надежности 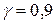 .
.
Найдем доверительный интервал для математического ожидания 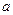 с надежностью 0,9, используя формулу:
с надежностью 0,9, используя формулу:
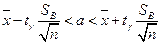 ,
,
где 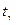 определяется из таблицы Стьюдента
определяется из таблицы Стьюдента 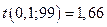 . Получаем после подстановки известных данных:
. Получаем после подстановки известных данных:
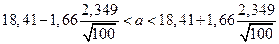
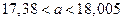 .
.
Доверительный интервал для неизвестной дисперсии 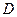 нормально распределенной случайной величины
нормально распределенной случайной величины 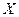 с доверительной вероятностью
с доверительной вероятностью 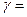 0,9 можно найти по формуле:
0,9 можно найти по формуле:
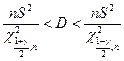
Находим значения из таблицы распределения 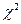 :
:
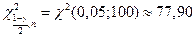 ,
, 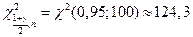 .
.
Получаем:
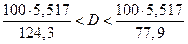 ,
,
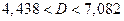 .
.
Тогда 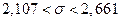 .
.
 2015-05-18
2015-05-18 11377
11377






