Рассмотрим квадратное уравнение
ах2 + bх + с = 0, а ≠ 0.
Умножая обе его части на а, получаем уравнение
а2 х2 + а bх + ас = 0.
Пусть ах = у, откуда х = 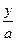 ; тогда приходим к уравнению
; тогда приходим к уравнению
у2 + by + ас = 0,
равносильного данному. Его корни у1 и у2 найдем с помощью теоремы Виета. Окончательно получаем х1 = 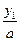 и х1 =
и х1 = 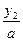 . При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
. При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его и называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.
Пример
2х2– 11х + 15 = 0, «перебросим» коэффициент 2 к свободному члену:
у2– 11у + 30 = 0, согласно теореме Виета найдем корни:
у1у2= 30 и у1+ у2= 11,
у1= 5 и у2= 6, окончательно получим:
х1= 5/2 и х2= 6/2,
х1= 2,5 и х2= 3.
Ответ: 2,5 и 3.
3.5 Решение квадратных уравнений с помощью номограммы:
Это старый и незаслуженно забытый способ решения квадратных уравнений, о котором рассказывается в Таблице XXII Четырехзначных математических таблиц, автор Брадис В.М. Номограмма для решения уравнения z2 + рz + q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения. Криволинейная шкала номограммы построена по формулам ОВ = 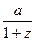 , АВ =
, АВ = 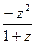 .
.
Полагая, что ОС = р, ЕД =q, ОЕ = а, из подобия треугольников САН и СДF получим пропорцию 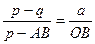 . Подставив, ОВ =
. Подставив, ОВ = 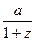 , АВ =
, АВ = 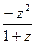 , получим
, получим 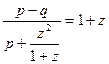
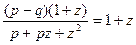 1+z
1+z 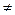 0
0
p – q = p + pz +z 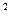
z  + pz + q = 0
+ pz + q = 0
Из пропорции после подстановок и упрощений получаем уравнение z2 + рz + q = 0, причем буква z означает метку любой точки криволинейной шкалы.

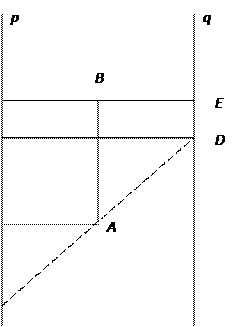 | |||
 | |||
| |||
х 2 – 9х + 8 = 0
Соединим b=-9 и c=8, номограмма даёт корни: х1 = 8 и х2 = 1
Из эксперимента:
2х2 – 9х + 4 = 0 /:2
х2 - 4,5х + 2 = 0
Соединим b=-4,5 и c=2, номограмма даёт корни: х1 = 4 и х2 = 0,5
 2015-05-18
2015-05-18 2670
2670
