Неопределенный интеграл

Пусть дана функция 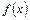. Функция 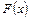называется первообразной для подынтегральной функции 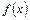или интегралом от 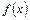, если 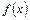является производной для функции 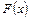, т.е. 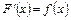и 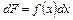. Например, для функции 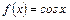первообразной будет функция 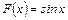, т.к. .

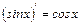Если 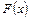является первообразной для 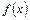, то и 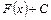, где 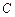- произвольная константа, также будет являться первообразной для 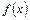, поскольку производная от константы равна нулю. Совокупность всех первообразных функций для функции 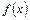называется неопределенным интегралом и обозначается 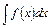. Таким образом:

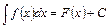. (1)

Из определения неопределенного интеграла вытекают формулы:

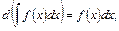(2)

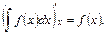(3)

Формула (3) может быть использована для проверки правильности интегрирования.

Геометрически неопределенный интеграл можно интерпретировать как бесконечное множество кривых 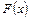, сдвинутых относительно друг друга на произвольную константу вдоль оси .

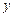2. Формулы интегрирования и таблица основных интегралов.

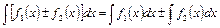
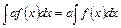, а – константа.

1. .

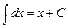2. , .

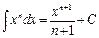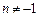3. .

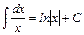4. .

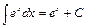5. .

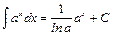6. .

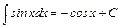7. .

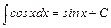8. .

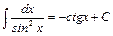9. .

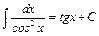10. .

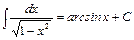11. .

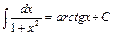Вычисление любого сложного интеграла, выражающегося через элементарные функции путем преобразований (если это необходимо), сводится к вычислению интегралов, представленных в таблице. Если интеграл табличный, то интегрирование осуществляется сразу.

Пример 1. Вычислить интеграл

.

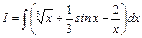Разбиваем интеграл на три интеграла и интегрируем:

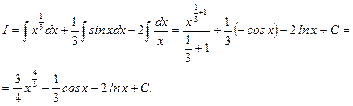
Дифференцированием первообразной проверим правильность интегрирования:

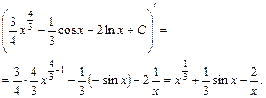
Полученное выражение совпадает с подынтегральной функцией, т.е. интегрирование проведено правильно.