Определенный интеграл

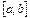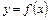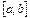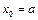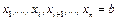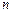Пусть дана непрерывная на отрезке функция . Разобьем точками , на отрезков длиной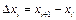 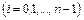(рис. 1) и составим сумму

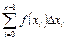, (13)

которая называется интегральной суммой для функции 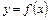на отрезке .

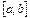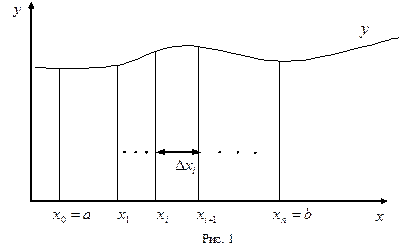
Каждое слагаемое этой суммы приближенно равно площади прямоугольника высотой 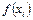и с основанием 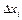, поэтому вся сумма (13) будет приближенно равна площади криволинейной трапеции, ограниченной прямыми 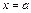, , 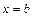отрезком 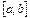на оси 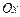и кривой .

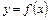Если функция 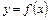непрерывна на отрезке 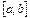, то при всех 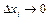существует предел суммы (13), не зависящий от способа разбиения отрезка 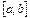. Этот предел называется определенным интегралом от функции 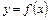на отрезке 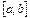и обозначается 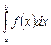. Т.о.:

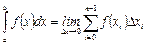(14)

и формула (14) дает точное значение площади криволинейной трапеции.

Определенный интеграл вычисляется по формуле Ньютона – Лейбница:

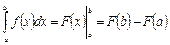, (15)

где 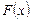- первообразная для функции .

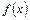Пример 11. Вычислить определенный интеграл

.

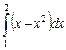Используя формулу (15), получим:

.

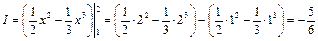При интегрировании по частям определенного интеграла справедлива формула:

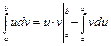. (15а)