Метод подстановки заключается в том, что переходя от переменной  к новой переменной
к новой переменной 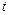 с помощью равенства
с помощью равенства 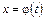 или
или 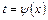 , где
, где 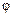 и
и 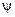 - некоторые дифференцируемые (за исключением, быть может, конечного числа точек) функции, получаем более простую подынтегральную функцию, интеграл от которой вычислить легче, чем от исходной функции.
- некоторые дифференцируемые (за исключением, быть может, конечного числа точек) функции, получаем более простую подынтегральную функцию, интеграл от которой вычислить легче, чем от исходной функции.
Пример 2. Вычислить интеграл 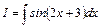 . Здесь необходимо упростить аргумент синуса, поэтому делаем подстановку:
. Здесь необходимо упростить аргумент синуса, поэтому делаем подстановку:
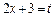 ;
; 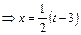 ;
; 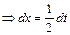 .
.
После подстановки исходный интеграл сводится к табличному:
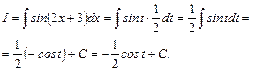 .
.
В этом примере мы использовали подстановку 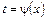 , где
, где 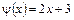 .
.
Пример 3. Вычислить интеграл
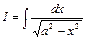 .
.
Делаем подстановку:
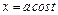 ;
; 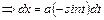 ;
; 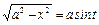 .
.
В результате интеграл 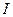 запишется в виде:
запишется в виде:
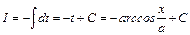 .
.
В данном примере использовалась подстановка 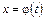 , где
, где 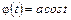 .
.
 2015-05-18
2015-05-18 256
256








