Интегралы вида
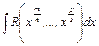 ,
,
где 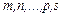 - целые числа, сводятся к интегралу от рациональных функций заменой переменной
- целые числа, сводятся к интегралу от рациональных функций заменой переменной 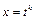 , где
, где 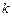 - наименьшее общее кратное чисел
- наименьшее общее кратное чисел  (НОК
(НОК 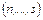 ). Аналогичная подстановка делается, если вместо
). Аналогичная подстановка делается, если вместо  содержатся выражения вида
содержатся выражения вида 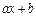 или
или 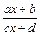 .
.
Пример 8. Вычислить интеграл
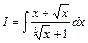 .
.
Т.к. НОК (2;3)=6, то делаем подстановку:
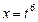
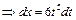 и
и
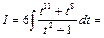
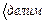
 =
=
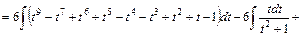
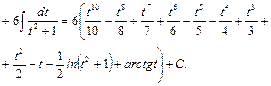
Переходя к переменной  , получим:
, получим:
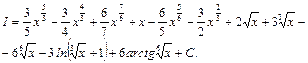
Интегралы вида 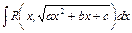 , где
, где 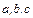 - вещественные числа, в общем случае вычисляются одной из подстановок Эйлера:
- вещественные числа, в общем случае вычисляются одной из подстановок Эйлера:
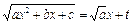 ,
, 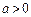 ; (9)
; (9)
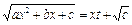 ,
, 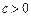 ; (10)
; (10)
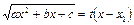 или
или 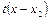 , (11)
, (11)
где 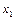 и
и 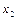 - различные вещественные корни трехчлена
- различные вещественные корни трехчлена 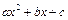 .
.
Пример 9. Вычислить интеграл
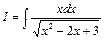 .
.
Используем 1–ю подстановку Эйлера (9): 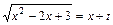 . Возведем в квадрат обе части равенства. После сокращения
. Возведем в квадрат обе части равенства. После сокращения 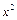 получим:
получим:
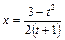
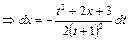 ;
;
выразим теперь радикал через переменную 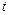 :
:
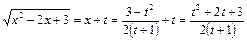 .
.
Подставляя выраженные через 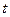 величины в
величины в 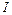 , получим:
, получим:
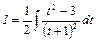 .
.
Делая подстановку 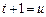 ;
; 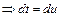 , получим:
, получим:
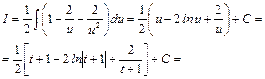
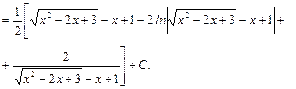
 2015-05-18
2015-05-18 577
577








