Самыми простыми дифференциальными уравнениями являются уравнения первого порядка:
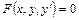 .
.
Определение. Частным решением уравнения первого порядка называется решение, удовлетворяющее заданному начальному условию
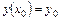 ,
,
где 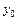 - заданная постоянная величина.
- заданная постоянная величина.
Самыми простыми дифференциальными уравнениями первого порядка являются уравнения вида
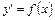 . (1)
. (1)
Такие уравнения решаются простым интегрированием функции, т.е.
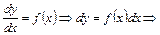
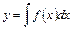 . (2)
. (2)
Следующими по сложности являются дифференциальные уравнения вида
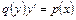 , (3)
, (3)
для которых дифференциальная форма такова:
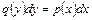 . (4)
. (4)
Поскольку в уравнении (4) левая часть содержит лишь переменную 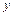 и ее дифференциал, а правая – лишь переменную
и ее дифференциал, а правая – лишь переменную  и ее дифференциал, то говорят, что в этом уравнении переменные
и ее дифференциал, то говорят, что в этом уравнении переменные  и
и 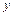 разделены.
разделены.
Чтобы решить уравнение (4), нужно проинтегрировать обе его части:
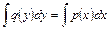 . (5)
. (5)
К решению уравнений вида (4) сводится интегрирование дифференциальных уравнений с разделяющимися переменными. Так называют уравнение
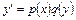 , (6)
, (6)
правая часть которого является произведением функции от  на функцию от
на функцию от  .
.
Пример 1. Решить уравнение
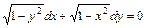 .
.
Решение. Это уравнение с разделяющимися переменными. Приведем его к виду (4), т.е. разделим переменные:
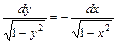 .
.
Получили уравнение с разделенными переменными. Проинтегрируем обе части полученного уравнения:
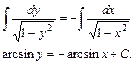 ;
;
В силу произвольности константы 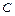 положим
положим 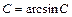 и запишем полученное равенство в виде:
и запишем полученное равенство в виде:
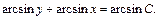
Из школьного курса алгебры известна формула:
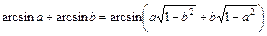 .
.
Тогда
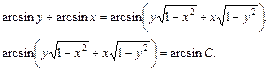
Окончательно будем иметь:
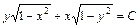 - общее решение (или общий интеграл) данного дифференциального уравнения.
- общее решение (или общий интеграл) данного дифференциального уравнения.
Ответ: 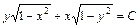 .
.
 2015-05-18
2015-05-18 275
275








