Рассмотрим еще один класс уравнений, которые путем подстановки сводятся к уравнениям с разделяющимися переменными.
Определение. Функция 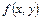 называется однородной функцией нулевой степени, если для любого
называется однородной функцией нулевой степени, если для любого 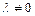 выполняется равенство
выполняется равенство
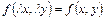 . (15)
. (15)
Иными словами, однородная функция нулевой степени не изменяется при умножении  и
и 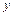 на одно и то же число.
на одно и то же число.
Определение. Дифференциальные уравнения 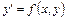 , правая часть которых является однородной функцией нулевой степени называются однородными уравнениями.
, правая часть которых является однородной функцией нулевой степени называются однородными уравнениями.
Однородные уравнения решаются с помощью замены 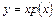 . Эта замена приводит однородные уравнения к уравнениям с разделяющимися переменными.
. Эта замена приводит однородные уравнения к уравнениям с разделяющимися переменными.
Пример 3. Решить уравнение 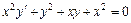 .
.
Решение. Разрешим данное уравнение относительно 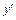 :
:
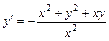 .
.
Это уравнение однородно, т.к. его правая часть – однородная функция нулевой степени.
Сделаем подстановку
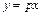 ,
,
тогда
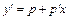 ,
,
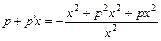 ,
,
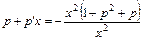 ,
,
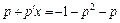 ,
,
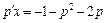 ,
,
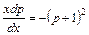 ,
,
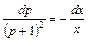 .
.
Получили уравнение с разделенными переменными. Проинтегрируем обе части этого уравнения:
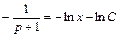 ,
,
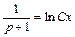 .
.
Сделаем обратную замену 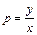 .
.
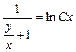 ,
,
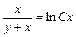 ,
,
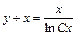 ,
,
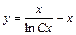 - общий интеграл.
- общий интеграл.
Ответ: 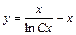 .
.
.
 2015-05-18
2015-05-18 428
428








