2015-05-18
566
Для выбора пути решения заданного дифференциального уравнения первого порядка сначала надо определить тип, к которому оно относится. Для этого следует разрешить данное уравнение относительно производной, т.е. привести его к виду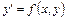 
. После этого надо посмотреть, не разлагается ли функция 
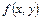на множители, один из которых зависит только от 
, а второй – только от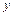 
. Если это возможно, то надо разделить переменные и интегрировать обе части получившегося равенства.
Если переменные не разделяются непосредственно, то следует проверить, является ли данное уравнение линейным или уравнением Бернулли, т.е. имеет ли функция 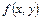вид 
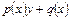или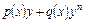 
.
К уравнению Бернулли также сводятся уравнения вида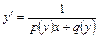 
(и более общего вида 
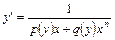). Для их решения надо поменять ролями переменные и 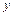и считать функцией от 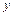. В результате для этой функции получим линейное уравнение: 
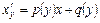(или уравнение Бернулли 
).
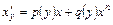Например, уравнение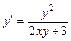 
, если 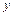считать аргументом, а - функцией, принимает вид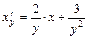 
, т.е. становится линейным.
Если и этот метод не приводит к цели, следует проверить, не является ли 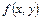однородной функцией нулевой степени.
|
|
|
Наконец, если и этот метод окажется неудачным, надо записать заданное уравнение в виде
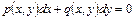
и проверить, не является ли оно уравнением в полных дифференциалах.
