2015-05-18
271
Определение. Линейным уравнением первого порядка называют дифференциальное уравнение первого порядка, которое линейно относительно функции и ее производной, т.е. уравнение вида
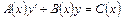. (7)
Здесь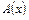 
, 
, 
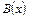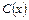- непрерывные функции от 
. В области, где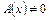 
, это уравнение равносильно уравнению вида
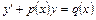. (8)
Проще всего решается линейное дифференциальное уравнение в том случае, когда его правая часть равна нулю, т.е. уравнения вида:
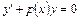. (9)
Такое уравнение называют однородным линейным уравнением первого порядка. Оно является уравнением с разделяющимися переменными.
Уравнение (8) в общем случае, т.е. когда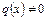 
, называют неоднородным линейным уравнением первого порядка. Такое уравнение решается с помощью замены
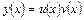. (10)
При этом уравнение (8) принимает вид:
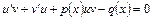. (11)
Бернулли доказал, что уравнение (11) разрешимо только в случае, если
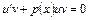. (12)
При выполнении равенства (12) из равенства (11) также следует, что
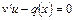. (13)
Таким образом, для решения уравнения (11) нужно сначала из уравнения (12) найти функцию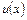 
, а затем, подставив найденную функцию в уравнение (13), найти функцию 
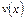, после чего подставить в равенство (10) эти две функции.
|
|
|
Пример 2. Найти общее решение уравнения 
.
Решение. Пусть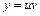 
, тогда 
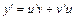. Данное уравнение примет вид:
.
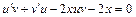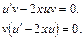
Так как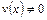 
, то
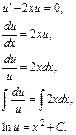
Найдем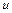 
из полученного равенства:
.
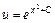В силу произвольности константы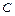 
положим 
.
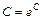Тогда
.
.
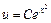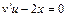Подставим в это равенство найденную функцию .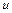
.
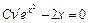Разделим переменные:
.
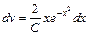Проинтегрируем обе части полученного равенства:
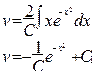
Подставим найденные функци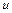и и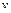 
в равенство (10):
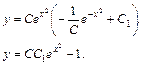
В силу произвольности констант 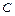и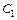 
положим 
.
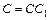Тогда искомое общее решение имеет вид:
.
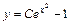Ответ: .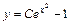
Подобным образом решается уравнение Бернулли:
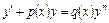. (14)
