Решите систему линейных уравнений тремя способами:
а) по формулам Крамера;
б) с помощью обратной матрицы;
в) методом Гаусса.
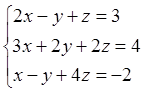
а) по формулам Крамера.
Решение:
Составим четыре определителя:
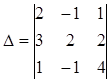 – главный, составлен из коэффициентов при неизвестных.
– главный, составлен из коэффициентов при неизвестных.
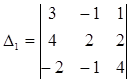 – составлен из главного, заменой столбца коэффициентов при х на столбец свободных членов, аналогично:
– составлен из главного, заменой столбца коэффициентов при х на столбец свободных членов, аналогично:
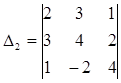 ;
; 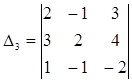
Вычисляем составленные определители по правилу треугольников:
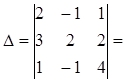 2·2·4 + (-1)·2·1 + 1·3·(-1) - 1·2·1 - 2·2·(-1) - (-1)·3·4 = 16 – 2 – 3 – 2 + 4 + 12 = 25 ≠ 0
2·2·4 + (-1)·2·1 + 1·3·(-1) - 1·2·1 - 2·2·(-1) - (-1)·3·4 = 16 – 2 – 3 – 2 + 4 + 12 = 25 ≠ 0
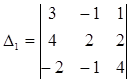 = 3·2·4 + (-1)·2·(-2) + 1·4·(-1) - 1·2·(-2) - 3·2·(-1) - (-1)·4·4 = 24 + 4 – 4 + 4 + 6 + 16 = 50
= 3·2·4 + (-1)·2·(-2) + 1·4·(-1) - 1·2·(-2) - 3·2·(-1) - (-1)·4·4 = 24 + 4 – 4 + 4 + 6 + 16 = 50
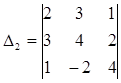 = 2·4·4 + 3·2·1 + 1·3·(-2) - 1·4·1 - 2·2·(-2) - 3·3·4 = 32 + 6 – 6 – 4 + 8 – 36 = 0
= 2·4·4 + 3·2·1 + 1·3·(-2) - 1·4·1 - 2·2·(-2) - 3·3·4 = 32 + 6 – 6 – 4 + 8 – 36 = 0
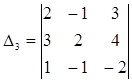 = 2·2·(-2) + (-1)·4·1 + 3·3·(-1) - 3·2·1 - 2·4·(-1) - (-1)·3·(-2) = - 8 – 4 – 9 – 6 + 8 – 6 = - 25
= 2·2·(-2) + (-1)·4·1 + 3·3·(-1) - 3·2·1 - 2·4·(-1) - (-1)·3·(-2) = - 8 – 4 – 9 – 6 + 8 – 6 = - 25
Находим решение по формулам Крамера:
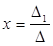 ;
; 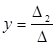 ;
; 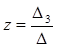 ;
;
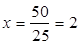 ;
; 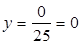 ;
; 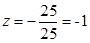 .
.
Проверка:
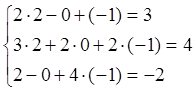
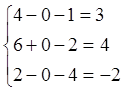
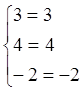
Ответ: 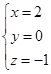 .
.
б) с помощью обратной матрицы.
Решение:
Составим три матрицы:
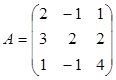 – из коэффициентов при неизвестных.
– из коэффициентов при неизвестных.
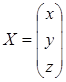 – столбцовая из неизвестных.
– столбцовая из неизвестных.
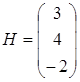 – из свободных членов.
– из свободных членов.
Систему можно записать в виде: 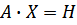 , где матрица Х находится по формуле
, где матрица Х находится по формуле 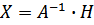 . Таким образом, нужно найти матрицу
. Таким образом, нужно найти матрицу 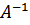 обратную для матрицы А.
обратную для матрицы А.
Находим определитель матрицы А:
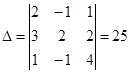 ≠ 0 => А невырожденная.
≠ 0 => А невырожденная.
Составим алгебраические дополнения элементов матрицы А:
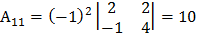 ;
;
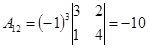 ;
;
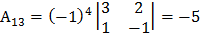
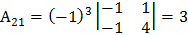
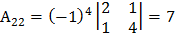
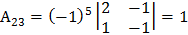
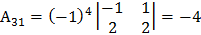
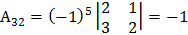
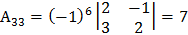
Составим матрицу В из полученных алгебраических дополнений:
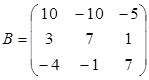 .
.
Составим транспонированную матрицу 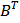 , заменив строки столбцами:
, заменив строки столбцами:
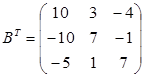 .
.
Обратную матрицу 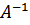 составим по формуле
составим по формуле 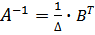 , таким образом:
, таким образом:
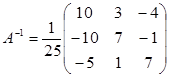 .
.
Найдем матрицу Х по формуле  :
:
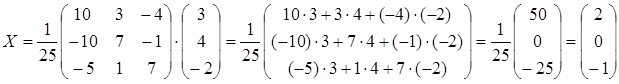 .
. 
Ответ: 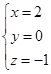 .
.
в) методом Гаусса.
Решение:
Расширенная матрица системы имеет вид:
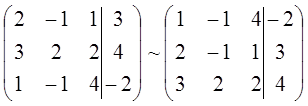
Используя элементарные преобразования, преобразуем расширенную матрицу системы.
1 шаг. Так как а11 = 1≠ 0, то умножая первую строку матрицы на числа (-2) и (-3) и прибавляя полученные строки соответственно ко второй и третьей строкам, исключим переменную х из всех строк, начиная со второй:
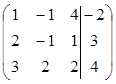 ~
~ 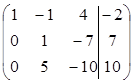 .
.
2 шаг. Так как теперь а22 = 1 ≠ 0, то умножая вторую строку на (-5) и прибавляя полученную строку к третьей, исключим из нее переменную у:
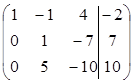 ~
~ 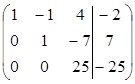 .
.
3 шаг. Получим следующую систему уравнений:
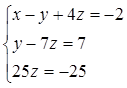 .
.
4 шаг. Используя обратный ход метода Гаусса, найдем из третьего уравнения 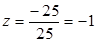 ; из второго
; из второго 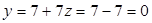 и из первого уравнения
и из первого уравнения 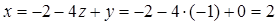 .
.
Ответ: 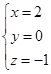 .
.
 2015-05-18
2015-05-18 416
416








