2015-05-18
1568
Исследуйте данную функцию и постройте ее график: у = 3х3 – 15х2 + 36.
При исследовании функции и построении их графиков рекомендуется использовать следующую схему:
1) Найти область определения функции.
2) Исследовать функцию на четность-нечетность.
3) Найти вертикальные асимптоты.
4) Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты.
5) Найти экстремумы и интервалы монотонности функции.
6) Найти интервалы выпуклости функции и точки перегиба.
7) Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.
Решение:
1) Функция определена на всей числовой прямой, т.е. D(у) = (-∞; +∞).
2) Данная функция не является ни четной, ни нечетной (функция общего вида):
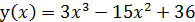
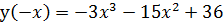
т.е у(-x) ≠ ± у(x):
3) Вертикальных асимптот нет, так как функция определена при всех действительных значениях х.
4) Поведение функции в бесконечности:
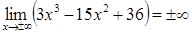, т.е. график данной функции асимптот не имеет.
5) Экстремумы и интервалы монотонности.
|
|
|
Находим первую производную:
;
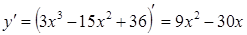у' = 0 при 9 х2 – 30 х = 0.
Решая данное уравнение, получим:
x(9x – 30)=0;
х1 = 0; х2 =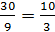 
,
т.е. критические точки х1 = 0, х2 =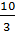 
. Эти точки делят область определения функции на три промежутка: (-∞; 0), (0; 
), (; +∞).
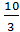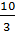| х | (-∞; 0), | х1 =0 | (0; )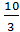
| х2 =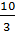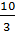
| (; +∞)
|
| у' | + | – | + | ||
| у |  
| mах | 
| min | 
|
В первом и последнем из них у'(x) > 0, в промежутке х є (0; 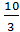) производная у'(x) < 0. Следовательно, в промежутках х є (-∞; 0), х є (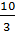; +∞) функция возрастает, а в промежутке х є (0; 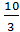) – убывает. При переходе через точку х1 производная меняет знак с плюса на минус, а при переходе через точку х2 – с минуса на плюс. То есть, х1 и х2 – точки экстремума. Находим значение функции в точках экстремума:
; 
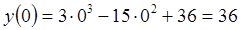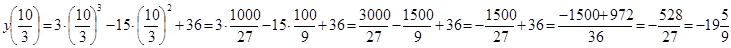Таким образом, (0;36) – точка максимума, (; – 
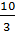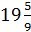) – точка минимума.
6) Интервалы выпуклости и точки перегиба.
Находим вторую производную:
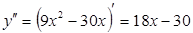; у'' = 0 при 18 х – 30 = 0; отсюда получаем х = 
.
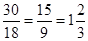Точка х =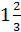 
делит область определения функции на два промежутка х є (-∞; )
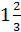и х є (; +∞).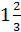
| х | (-∞; )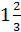
| х =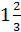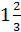
| (; +∞)
|
| у'' | – | + | |
| у | 
| точка перегиба | 
|
В первом из них у'' < 0, т.е. кривая выпукла вверх, а во втором у'' > 0, т.е. кривая выпукла вниз. Следовательно, точка х = 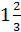является точкой перегиба. Находим значение функции в этой точке:
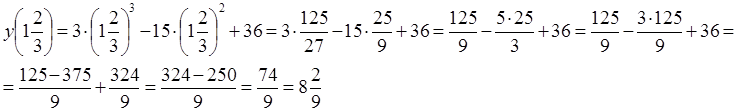Таким образом, (; 
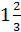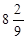) – точка перегиба.
7) Находим точку пересечения графика с осью ОУ: при х = 0 значение функции
.
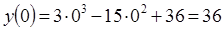Находим точки пересечения графика функции с осью ОХ. Решим кубическое уравнение у(х) = 0.
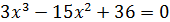
Попробуем разложить многочлен на множители по схеме Горнера. Для начала методом подбора найдем один корень. Обычно он является делителем свободного члена. В данном случае делителями числа 36 являются ±1, ±2, ±3, ±6, ±9, ±18, ±36.
|
|
|
Подставим число 1: 3*1-15*1+36 = 24. Мы выяснили, что число 1 не является корнем уравнения. Далее проверяем все делители, пока не найдем тот, который бы являлся корнем данного уравнения:
Число -1: 3*(-1)-15*1+36=18
Число 2: 3*8-15*4+36=0
Мы выяснили, что число 2 является корнем уравнения.
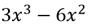Мы нашли один из корней многочлена. Корнем многочлена является число 2, а значит исходный многочлен должен делиться на x – 2, т.е.:
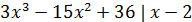
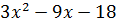
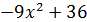
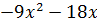
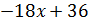
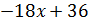
Таким образом, уравнение представляет собой произведение двух множителей:
)(
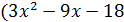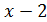) = 0
Первый корень у нас найден: x1 = 2. Найдем оставшиеся два корня. Для этого решим уравнение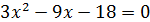 
Решая данное уравнение, получим:
D = (-9)2 – 4·3·(-18) = 81 + 216 = 297 = 9*33 = 32 * 33;
х2 =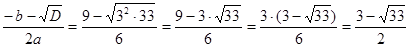 
;
х3 =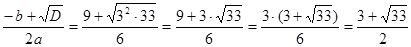 
.
Таким образом, функция пересекает ось ОХ в следующих точках: (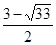
;0), (2;0) и (
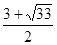;0)
По полученным точкам построим график данной функции: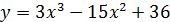 
ГРАФИК ПРИЛОЖЕН ОТДЕЛЬНЫМ ФАЙЛОМ
