Найдите пределы функций.
а) 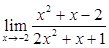 ;
;
Решение:
На основании непрерывности функции в точке х = 7 искомый предел равен значению функции в этой точке, т.е.
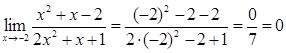 .
.
б) 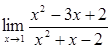 ;
;
Решение:
Для раскрытия неопределенности вида 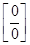 разложим числитель и знаменатель на множители и сократим дробь на множитель (х – 1):
разложим числитель и знаменатель на множители и сократим дробь на множитель (х – 1):
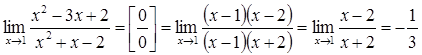 .
.
Здесь предварительно имеем 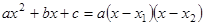 , где
, где 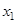 и
и 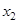 - корни квадратного трехчлена.
- корни квадратного трехчлена.
1) Числитель 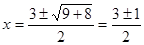 ;
; 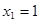 ;
; 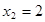 ;
;
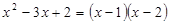 .
.
2) Знаменатель 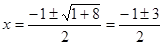 ;
; 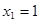 ;
; 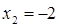 ;
;
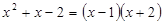 .
.
в) 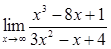 ;
;
Решение:
Имеем неопределенность вида 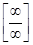 . Учитывая, что поведение числителя и знаменателя при х → ∞ определяется членами с наибольшими показателями степеней (соответственно х3 и 3х2), разделим числитель и знаменатель на х3, т.е. на х с наибольшим показателем степени числителя и знаменателя. Используя теоремы о пределах, получим:
. Учитывая, что поведение числителя и знаменателя при х → ∞ определяется членами с наибольшими показателями степеней (соответственно х3 и 3х2), разделим числитель и знаменатель на х3, т.е. на х с наибольшим показателем степени числителя и знаменателя. Используя теоремы о пределах, получим:
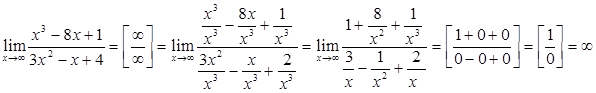 ,
,
так как
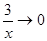 ;
; 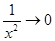 ;
; 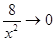 ;
; 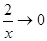 и
и 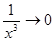 при
при 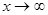 .
.
г) 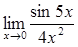 ;
;
Решение:
Имеем неопределенность вида 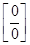 . Используя первый замечательный предел вида
. Используя первый замечательный предел вида 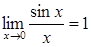 , получим:
, получим:
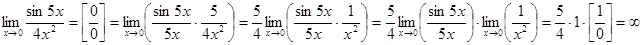 .
.
д) 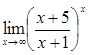
Решение:
Имеем неопределенность вида 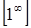 , так как
, так как 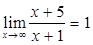 ,
, 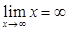 . Используя второй замечательный предел вида
. Используя второй замечательный предел вида 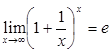 , выделим у дроби целую часть:
, выделим у дроби целую часть:
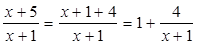 .
.
Тогда получим:
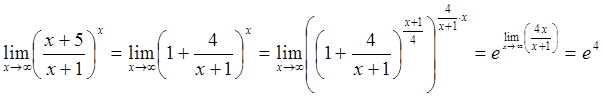 .
.
 2015-05-18
2015-05-18 435
435








