Задача о многомерном ранце имеет следующую математическую модель:
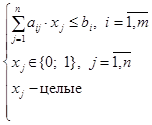 , (3)
, (3)
где критерием является функция
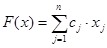 , (4)
, (4)
От задачи об одномерном ранце она отличается наличием нескольких ограничений. Таким образом, математическая модель:
Пусть 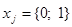 – j-тый город, откуда соответственно
– j-тый город, откуда соответственно 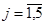 . При этом, если в j-тый город будет разгружаться алкогольная продукция, то
. При этом, если в j-тый город будет разгружаться алкогольная продукция, то 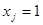 , иначе
, иначе 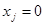 .
.
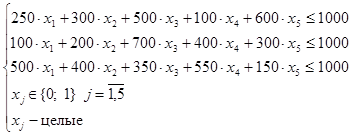 ;
;
Целевой функцией или критерием будет являться максимальная благодарность сограждан:
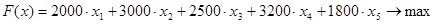 .
.
Решим задачу оценки критерия для каждого ограничения в отдельности. Пусть множество 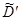 относится к первому ограничению,
относится к первому ограничению, 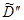 – ко второму, а
– ко второму, а  – к третьему.
– к третьему.
1) Анализ множества 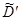 .
.
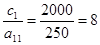 (3);
(3); 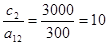 (2);
(2); 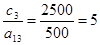 (4);
(4); 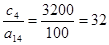 (1);
(1); 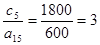 (5).
(5).
Определяем начальный план:
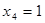 ,
, 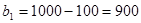 ;
;
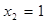 ,
, 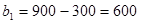 ;
;
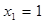 ,
, 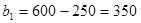 ;
;
В последнем случае оставшееся после других городов расстояние меньше 500 миль, поэтому 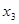 будет дробным:
будет дробным: 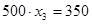 , =>
, => 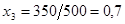 .
.
Таким образом, начальный опорный план: 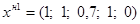 .
.
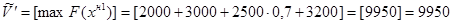 ;
;
2) Анализ множества 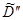 .
.
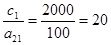 (1);
(1); 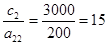 (2);
(2); 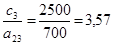 (5);
(5); 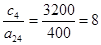 (3);
(3); 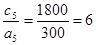 (4).
(4).
Определяем начальный план:
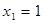 ,
, 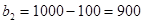 ;
;
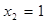 ,
, 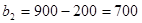 ;
;
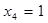 ,
, 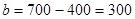 ;
;
В последнем случае оставшееся после других городов расстояние также равно 300 миль, поэтому 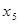 будет целым:
будет целым: 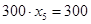 , =>
, => 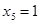 .
.
Таким образом, опорный план: 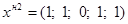 .
.
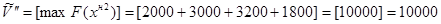 ;
;
3) Анализ множества  .
.
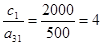 (5);
(5); 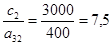 (2);
(2); 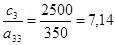 (3);
(3); 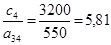 (4);
(4); 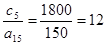 (1).
(1).
Определяем начальный план:
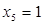 ,
, 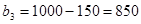 ;
;
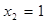 ,
, 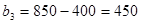 ;
;
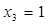 ,
, 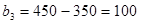 ;
;
В последнем случае оставшееся после других городов расстояние меньше 550 миль, поэтому 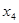 будет дробным:
будет дробным: 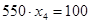 , =>
, => 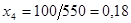 .
.
Таким образом, опорный план: 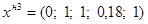 .
.
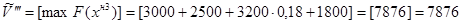 ;
;
 2015-05-18
2015-05-18 988
988








