Лабораторная работа № 6
Телешовой Елизаветы, гр. 726,
Решение задачи о ранце методом ветвей и границ.
Постановка задачи.
1929 год. В США великая депрессия, введен сухой закон. Страна просто задыхается без спиртного. В этот сложный момент группа инициативных граждан под руководством Аль Капоне решает помочь родной стране. Ими планируется поставка алкогольной продукции из Ливерпуля в Штаты. Благодарные сограждане из 5 крупных городов США готовы платить большие деньги за тонну спиртного: 2000 долл. в Бостоне, 3000 в Детройте, 2500 в Вашингтоне, 3200 в Нью-Йорке и 1800 долл в Чикаго. Все 5 городов находятся на разном расстоянии от порта, куда прибывает груз: Бостон – 250 миль, Детройт – 300 миль, Вашингтон – 500 миль, Нью-Йорк –100 миль и Чикаго – 600 миль. Требуется выбрать города, в которых можно получить максимальную прибыль от продажи спиртного. При этом суммарное расстояние от этих портов до порта с грузом не должно превышать 1000 миль.
Решение задачи.
Данная задача является задачей о ранце вида:
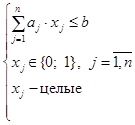 , (1)
, (1)
где критерием является функция
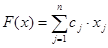 , (2)
, (2)
которая может быть устремлена и к максимуму, и к минимуму.
Для начала составим следующую математическую модель:
Пусть 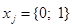 – j-тый город, откуда соответственно
– j-тый город, откуда соответственно 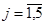 . При этом, если в j-тый город будет разгружаться алкогольная продукция, то
. При этом, если в j-тый город будет разгружаться алкогольная продукция, то 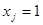 , иначе
, иначе 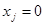 . Другим ограничением будет являться суммарное расстояние до порта с грузом. Таким образом:
. Другим ограничением будет являться суммарное расстояние до порта с грузом. Таким образом:
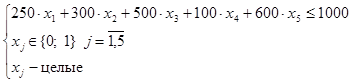 ;
;
Целевой функцией или критерием будет являться максимальная благодарность сограждан:
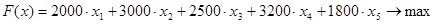 .
.
Далее отбираем порты по приоритетности, т.е. в порядке убывания отношения 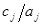 :
:
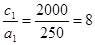 (3);
(3); 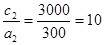 (2);
(2); 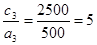 (4);
(4); 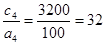 (1);
(1); 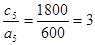 (5).
(5).
После этого определяем начальный план следующим образом: пусть 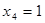 , поскольку отношение
, поскольку отношение 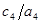 наибольшее, и следовательно продажа спиртного в Нью-Йорке даст наибольшую прибыль при наименьших затратах, которые зависят от расстояния. Вычитая из суммарного расстояния
наибольшее, и следовательно продажа спиртного в Нью-Йорке даст наибольшую прибыль при наименьших затратах, которые зависят от расстояния. Вычитая из суммарного расстояния 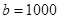 расстояние до порта мы получим расстояние, которое разделяется между остальными городами, т.е.:
расстояние до порта мы получим расстояние, которое разделяется между остальными городами, т.е.:
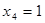 ,
, 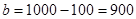 ;
;
Аналогично рассуждая, далее получаем:
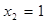 ,
, 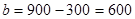 ;
;
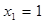 ,
, 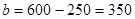 ;
;
В последнем случае оставшееся после других городов расстояние меньше 500 миль, поэтому 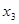 будет дробным:
будет дробным: 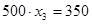 , =>
, => 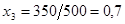 .
.
Таким образом, начальный опорный план: 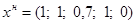 .
.
Значение целевой функции: 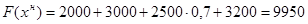 .
.
Но 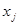 обязательно целое. Поэтому чтобы определить, чему все же равен
обязательно целое. Поэтому чтобы определить, чему все же равен 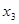 : 0 или 1 вычислим следующие значения:
: 0 или 1 вычислим следующие значения:
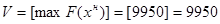 ;– целая часть критерия при существующем опорном плане.
;– целая часть критерия при существующем опорном плане.
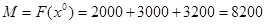 ;– значение критерия при целочисленном опорном плане, т.е.
;– значение критерия при целочисленном опорном плане, т.е. 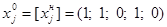 .
.
Множество D, которому принадлежит 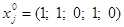 имеет
имеет 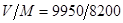 ,
, 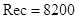 . Разделим его на 2 подмножества, такие что:
. Разделим его на 2 подмножества, такие что:
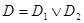 ;
;
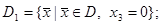 - здесь
- здесь 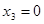 .
.
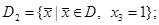 - здесь
- здесь 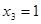 .
.
1) Анализ множества D1.
Поскольку 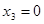 целевая функция и ограничения будут иметь вид:
целевая функция и ограничения будут иметь вид:
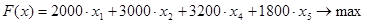
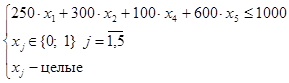
Строим новый опорный план:
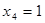 ,
, 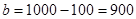 ;
;
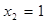 ,
, 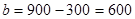 ;
;
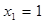 ,
, 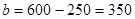 ;
;
Т.к. 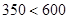 , поэтому
, поэтому 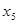 будет дробным:
будет дробным: 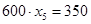 , =>
, => 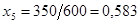 .
.
Таким образом, новый опорный план: 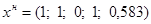 .
.
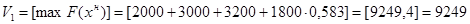 ;
;
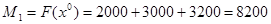 , при
, при 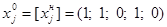 .
.
2) Анализ множества D2.
Поскольку 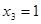 целевая функция и ограничения будут иметь вид:
целевая функция и ограничения будут иметь вид:
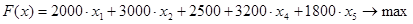
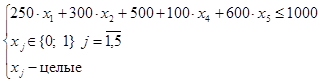 =>
=> 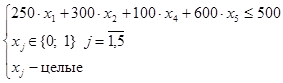 .
.
Строим новый опорный план:
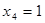 ,
, 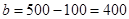 ;
;
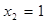 ,
, 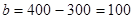 ;
;
Т.к. 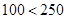 , поэтому
, поэтому 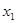 будет дробным:
будет дробным: 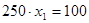 , =>
, => 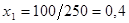 .
.
Таким образом, новый опорный план: 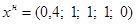 .
.
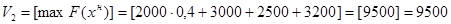 ;
;
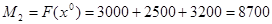 , при
, при 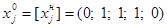 .
.
 2015-05-18
2015-05-18 306
306







