Среднее квадратичное отклонение и дисперсия случайной величины

Пример 2. Найдем математическое ожидание случайных величин 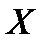и 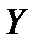, зная законы их распределения

1)

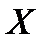	-8	-4	-1
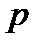	1/12	1/6	1/4	1/6	1/12	1/4

2)

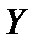	-2	-1
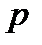	1/6	1/6	1/12	1/3		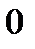1/4

Решение: , .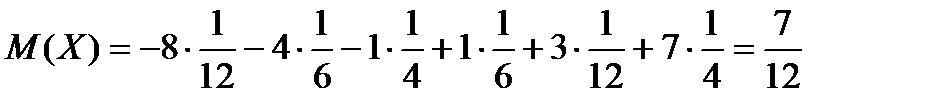

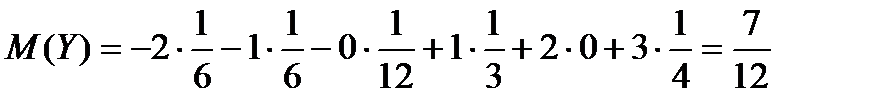a)

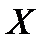Получили любопытный результат: законы распределения величин и 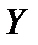разные, а их математические ожидания одинаковы.

б)

Из рисунка б видно, что значение величины 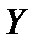более сосредоточены около математического ожидания 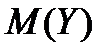, чем значения величины 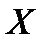, которые разбросаны (рассеяны) относительно ее математического ожидания 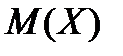(рисунок а).

Основной числовой характеристикой степени рассеяния значений случайной величины 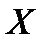относительно ее математического ожидания 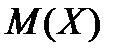является дисперсия, которая обозначается через .

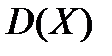Определение.Отклонением называется разность между случайной величиной 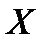и ее математическим ожиданием 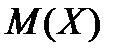, т.е. .

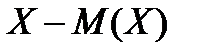Отклонение 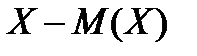и его квадрат 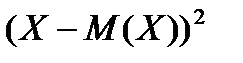также являются случайными величинами.

Определение. Дисперсией дискретной случайной величины 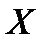называется математическое ожидание квадрата ее отклонения: .

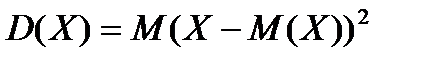Свойства дисперсии.

1. Дисперсия постоянной величины С равна 0: .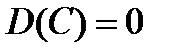

2. Если 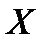- случайная величина, а С – постоянная, то , .

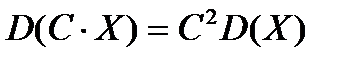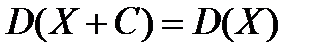3. Есл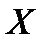и и 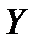- независимые случайные величины, то .

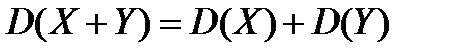Для вычисления дисперсий более удобной является формула .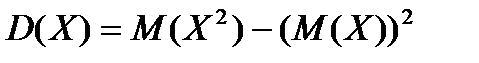

Пример 3. Дискретная случайная величина распределена по закону:

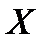	-1
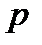	0,2	0,1	0,3	0,4

Найти .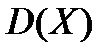

Решение. Сначала находим . ,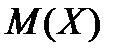

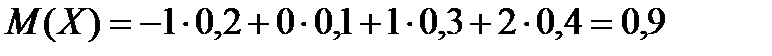а затем . .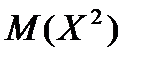

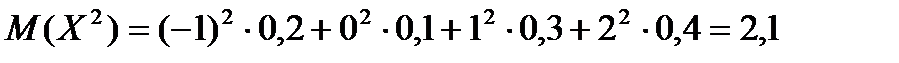По формуле 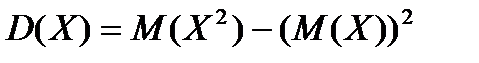имеем .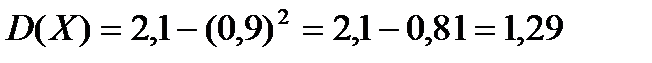

Средним квадратичным отклонением случайной величины называется корень квадратный из ее дисперсии: .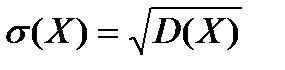

Содержание работы.

Задание 1. Используя классическое определение вероятности, решите задачи:

1.1. В ящике имеется 50 одинаковых деталей, из них 5 окрашенных. Наудачу вынимают одну деталь. Найти вероятность того, что извлеченная деталь окажется окрашенной.

1.2. Брошена игральная кость. Найти вероятность того, что выпадет четное число очков.

1.3. Участники жеребьевки тянут из ящика жетоны с номерами от 1 до 100. Найти вероятность того, что номер первого наудачу извлеченного жетона не содержит цифры 5.

1.4. В мешочке имеется 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв: о, п, р, с, т. Найти вероятность того, что на вынутых по одному и расположенных «в одну линию» кубиков можно будет прочесть слово «спорт».

1.5. Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик будет иметь одну окрашенную грань

Задание 2. Используя теорему сложения вероятностей, решите задачи:

2.1. В денежно-вещевой лотерее на каждые 10 000 билетов разыгрывается 150 вещевых и 50 денежных выигрышей. Чему равна вероятность выигрыша, безразлично денежного или вещевого, для владельца одного лотерейного билета?

2.2. Вероятность того, что стрелок при одном выстреле выбьет 10 очков, равна 0,1; вероятность выбить 9 очков равна 0,3; вероятность выбить 8 или меньше очков равна 0,6. Найти вероятность того, что при одном выстреле стрелок выбьет не менее 9 очков.

2.3. В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди наудачу извлеченных 2 деталей есть хотя бы одна стандартная.

2.4. В ящике 10 деталей, среди которых 2 нестандартных. Найти вероятность того, что в наудачу отобранных 6 деталях окажется более одной нестандартной детали.

2.5. События А, В, С и D образуют полную группу. Вероятности событий таковы: Р(А)=0,1; Р(В) = 0,4; Р(С)=0,3. Чему равна вероятность события D?

Задание 3. Используя теорему умножения вероятностей, решите задачи:

3.1. Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго – 0,8, для третьего – 0,9. Определите вероятность того, что в цель попадет хотя бы один стрелок.

3.2. Вероятность того, что стрелок при одном выстреле попадет в мишень, равна р=0,9. Стрелок произвел три выстрела. Найти вероятность того, все 3 выстрела дали попадание.

5.3. Три стрелка независимо друг от друга стреляют по цели. Вероятность попадания в цель для первого стрелка равна 0,75, для второго – 0,8, для третьего – 0,9. Определите вероятность того, что все три стрелка одновременно попадут в цель.

3.4. В первом ящике имеются 2 белых и 10 черных шаров; во втором ящике 8 белых и 4 черных шара. Из каждого ящика извлекли по шару. Какова вероятность, того, что оба шара белые?

3.5. Брошены монета и игральная кость. Найти вероятность совмещения событий: «появился «герб», «появилось 6 очков».

Задание 4. Найдите математическое ожидание дискретной случайной величины X, заданной законом распределения:

4.1

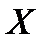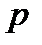	0,2	0,3	0,5

4.2

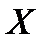	0,21	0,54	0,61
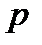	0,1	0,5	0,4

4.3

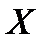	0,2	0,5	0,6
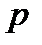	0,1	0,5	0,4

4.4

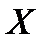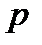	0,2	0,3	0,5

4.5

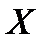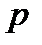	0,4	0,5	0,1

Задание 5. Найдите математическое ожидание случайной величины Z, если известны математические ожидания X и Y:

5.1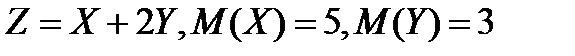

5.2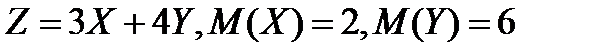

5.3.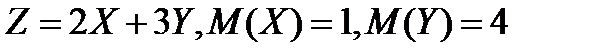

5.4.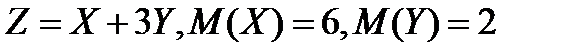

5.5.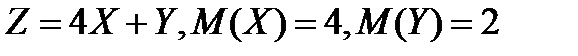

Задание 6. Найдите дисперсию и среднее квадратичное отклонение дискретной случайной величины X, заданной законом распределения:

6.1

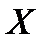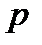	0,05	0,10	0,25	0,6

6.2

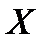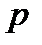	0,4	0,3	0,1	0,2

6.3

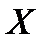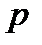	0,3	0,4	0,1	0,2

6.4

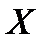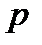	0,1	0,6	0,1	0,2

6.5

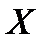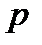	0,15	0,55	0,1	0,2

Вопросы для самоконтроля.

1. Какое событие называют достоверным? Невозможным?
2. Какими свойствами обладают события, образующие полную систему событий?
3. Что называется вероятностью события?
4. Сформулируйте теорему сложения независимых событий.
5. Чему равна сумма вероятностей противоположных событий?
6. Сформулируйте теорему умножения вероятностей независимых событий.
7. Напишите формулу полной вероятности. Объясните все обозначения, входящие в эту формулу.
8. В ящике лежат 90 шаров, 18 из них – цветные. Найдите вероятность того, что вытащенный наугад шар – цветной.
9. Приведите пример какой-нибудь случайной величины.
10. Что называется распределением случайной величины?
11. Какое распределение называется биномиальным?
12. Дайте определение математического ожидания случайной величины.
13. Что называется дисперсией случайной величины?
14. Как связаны между собой M(X), M(X²), D(X)?

Таблица распределения заданий по вариантам.

№ Практической работы.	№ задания в практической работе	Вариант № 1	Вариант № 2	Вариант № 3	Вариант № 4	Вариант № 5
П.Р. №1	Задание 1.	1.1.;2.1; 3.1; 4.1; 5.1	1.2; 2.2; 3.2; 4.2; 5.2	1.3; 2.3; 3.3; 4.3; 5.3	1.4; 2.4; 3.4; 4.4; 5.4	1.5; 2.5; 3.5; 4.5; 5.5
Задание 2.
Задание 3	1.1; 2.1; 3.1; 4.1	1.2; 2.2; 3.2; 4.2	1.3; 2.3; 3.3; 4.3	1.4; 2.4; 3.4; 4.4	1.5; 2.5; 3.5; 4.5
Задание 4
Задание 5	1.1-1.7 для №1	1.1-1.7 для №2	1.1-1.7 для №3	1.1-1.7 для №4	1.1-1.7 для №5
П.Р. №2	Задание 1.	1.1	1.2	1.3	1.4	1.5
Задание 2.	2.1	2.2	2.3	2.4	2.5
Задание 3	3.1	3.2	3.3	3.4	3.5
Задание 4	4.1	4.2	4.3	4.4	4.5
Задание 5	5.1	5.2	5.3	5.4	5.5
Задание 6	6.1	6.2	6.3	6.4	6.5
Задание 7	7.1	7.2	7.3	7.4	7.5
Задание 8	8.1	8.2	8.3	8.4	8.5
П.Р. №3	Задание 1.	1.1	1.2	1.3	1.4	1.5
Задание 2.	2.1	2.2	2.3	2.4	2.5
Задание 3	3.1	3.2	3.3	3.4	3.5
Задание 4	4.1	4.2	4.3	4.4	4.5
Задание 5	5.1	5.2	5.3	5.4	5.5
Задание 6	6.1	6.2	6.3	6.4	6.5
П.Р. №4	Задание 1.	1.1	1.2	1.3	1.4	1.5
Задание 2.
Задание 3
Задание 4
П.Р. №5	Задание 1.	1.1	1.2	1.3	1.4	1.5
Задание 2.	2.1	2.2	2.3	2.4	2.5
Задание 3	3.1	3.2	3.3	3.4	3.5
П.Р. №6	Задание 1.	1.1	1.2	1.3	1.4	1.5
Задание 2.	2.1	2.2	2.3	2.4	2.5
Задание 3	3.1	3.2	3.3	3.4	3.5
Задание 4	4.1	4.2	4.3	4.4	4.5
Задание 5	5.1	5.2	5.3	5.4	5.5
П.Р. №7	Задание 1.
Задание 2.
Задание 3
П.Р. №8	Задание 1.	1.1	1.2	1.3	1.4	1.5
Задание 2.	2.1	2.2	2.3	2.4	2.5
Задание 3	3.1	3.2	3.3	3.4	3.5
П.Р. №9	Задание 1.	1.1	1.2	1.3	1.4	1.5
Задание 2.	2.1	2.2	2.3	2.4	2.5
Задание 3	3.1	3.2	3.3	3.4	3.5
Задание 4	4.1	4.2	4.3	4.4	4.5
Задание 5	5.1	5.2	5.3	5.4	5.5
Задание 6	6.1	6.2	6.3	6.4	6.5
П.Р. №10	Задание 1.	1.1	1.2	1.3	1.4	1.5
Задание 2.	2.1	2.2	2.3	2.4	2.5
Задание 3	3.1	3.2	3.3	3.4	3.5
Задание 4	4.1	4.2	4.3	4.4	4.5
Задание 5	5.1	5.2	5.3	5.4	5.5
Задание 6	6.1	6.2	6.3	6.4	6.5