Явления объективного мира, включая медико-биологические, находятся в причинно-следственных отношениях В научной и практической работе врача статистические методы изучения связей применяют при исследовании: взаимосвязи между отдельными признаками физического развития; влияния факторов внешней среды (температура, влажность, давление и т.д.) на деятельность органов и систем; влияния условий труда и быта населения на уровень и изменения его здоровья и т.д. В медико-биологических процессах отмечаются корреляционные связи, т.е. такие связи, при которых каждому значению одного признака может соответствовать не одно единственное значение, а некоторое количество значений другого признака, варьирующих в определенных пределах.
Существуют различные способы определения размера корреляционной связи в изучаемой совокупности. Выбор способа зависит от числа наблюдений и от характера корреляционной связи. При большом числе наблюдений корреляционную связь рассчитывают при помощи корреляционной решетки (например, при изучении физического развития населения). При небольшом числе наблюдений (до 30 пар чисел) выбор способа зависит от характера связи. Существуют прямолинейная, криволинейная и множественная корреляция.
|
|
|
При измерении связи между изучаемыми явлениями определяют форму и тесноту связи. По форме корреляционная связь может быть прямой или обратной. При прямой связи с увеличением факториального признака увеличивается результативный и, наоборот, при обратной связи с увеличением факториального признака уменьшается результативный.
Мерой измерения тесноты корреляционной связи служит коэффициент корреляции. Значение коэффициента корреляции колеблется в пределах от 0 до 1 (знак "+"- прямая связь, знак "–" - обратная связь) и отражает степень связи:
от 0 до 0,30 слабая связь между явлениями;
от 0,31 до 0,70 - средняя связь между явлениями;
от 0,71 до 0,99 - сильная связь между явлениями.
Коэффициент корреляции Пирсона – наиболее известен и рассчитывается по формуле:
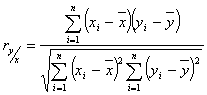 (22)
(22)
где
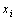 - конкретные значения одного признака;
- конкретные значения одного признака;
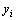 - конкретные значения второго признака;
- конкретные значения второго признака;
`x и `y - средние значения признаков;
n - число пар наблюдений.
Оценка достоверности выборочных коэффициентов корреляции производится с помощью вычисления их ошибок или по специальной таблице.
При числе парных наблюдений n > 100 ошибка коэффициента корреляции определяется как:
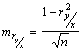 (23)
(23)
и коэффициент корреляции считается достоверным, если он превышает свою ошибку в 3 и более раза.
При числе парных наблюдений n < 100 ошибка вычисляется по формуле:
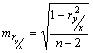 (24)
(24)
а оценка достоверности производится с помощью t - критерия:
|
|
|
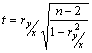 (25)
(25)
Полученную величину t сравнивают с табличными значениями 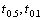 или
или 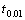 при числе степеней свободы n = n - 2. Если полученное значение t >
при числе степеней свободы n = n - 2. Если полученное значение t > 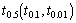 , коэффициент корреляции считается достоверным с вероятностью 95 %, 99 % или 99,9 %.
, коэффициент корреляции считается достоверным с вероятностью 95 %, 99 % или 99,9 %.
При небольшом числе сравниваемых пар, а также в случаях, когда исследуемые данные носят приближенный характер или выражаются атрибутивными признаками различной интенсивности, целесообразно использовать непараметрический коэффициент связи - коэффициент ранговой корреляции Спирмена (P), вычисляемый по формуле:
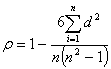 (26)
(26)
где
r - коэффициент ранговой корреляции ("ро");
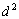 - квадраты разностей рангов изучаемых признаков;
- квадраты разностей рангов изучаемых признаков;
n - число парных наблюдений.
В углубленных исследованиях может быть рекомендован коэффициент корреляции рангов Кэндела, так как критерии оценки значимости этого коэффициента теоретически более обоснованы. Методики расчета коэффициентов корреляции подробно изложены в доступной литературе [20,21].
Коэффициенты корреляции позволяют измерить степень связи между признаками (явлениями), определить ее направление и форму. Представление же о том, как в среднем может измениться один варьирующий признак при изменении другого, связанного с ним признака, может дать только регрессионный анализ.
Коэффициент регрессии вычисляется по формуле:
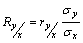 (27)
(27)
где
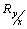 - коэффициент регрессии;
- коэффициент регрессии;
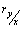 - коэффициент корреляции;
- коэффициент корреляции;
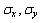 - средние квадратические отклонения признаков.
- средние квадратические отклонения признаков.
 2015-05-20
2015-05-20 767
767








