Записать интерполяционную формулу Лагранжа

Поставим задачу. Требуется найти алгебраический многочлен 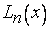степени не выше, чем 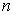, который совпадал бы с функцией 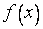в заданных точках 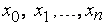. Таким образом, должны выполняться условия

.

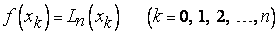Многочлен 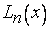единственный. Если предположить, что существует еще один многочлен 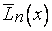с теми же свойствами, то разность 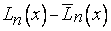обратится в нуль в 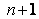точке 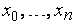и будет алгебраическим многочленом степени не выше, чем 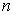, значит, разность тождественно равна нулю и .

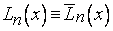Из единственности следует, что если исходная функция 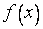сама является алгебраическим многочленом степени 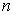, то она совпадает с 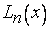для всех .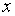

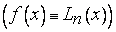Сначала найдем алгебраический многочлен степени 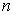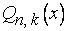, который в точках 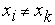равен нулю, а в точке 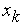равен единице. Очевидно, что

,

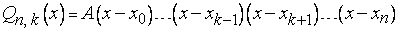где постоянная 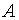находится из условия

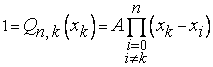, т. е. .

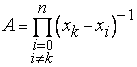Таким образом, искомый многочлен имеет вид

.

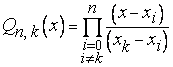Если ввести в рассмотрение символ Кронекера

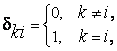
то

.

Поставленную задачу решает многочлен

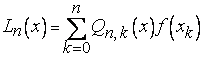, (1)

ибо

.

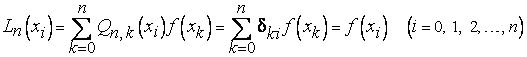Многочлен (1) называется интерполяционным многочленом Лагранжа.